Площадь прямоугольника онлайн

Площадь прямоугольника

Определение Площадь прямоугольника – это пространство, ограниченное сторонами прямоугольника, то есть в пределах периметра прямоугольника.

Формулы определения площади прямоугольника

1. Формула для площади двустороннего прямоугольника:

S = ab

2. Формула площади прямоугольника по периметру и любой стороне:

S =	Па – 2a2	=	Pb – 2b2
2	2

3. Формула площади прямоугольника по диагонали и любой стороне:

S = a√d2 – a2 = b√d2 – b2

4. Формула площади прямоугольника через диагональ и синус острого угла между диагоналями:

S =	d2 грех β
2

5. Формула площади прямоугольника через радиус описанной окружности и любой стороны:

S = a√4R2 – a2 = b√4R2 – b2

6. Формула площади прямоугольника через диаметр описанной окружности с любой стороной:

S = a√Do2 – a2 = b√Do2 – b2

Необходимость расчета диагонали фундамента

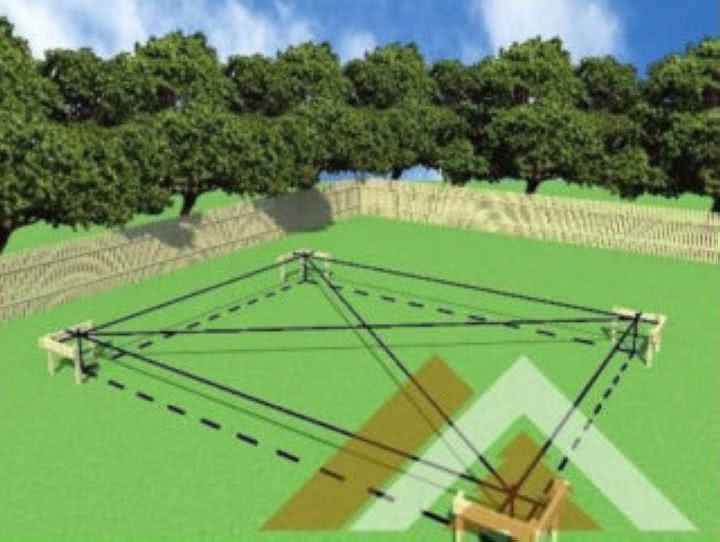
Если диагональ рассчитана неправильно, все дальнейшие конструкции будут отклоняться от плоскости

Проект предполагает подбор элементов конструкции ровно по размеру, чтобы при строительстве не было перекосов. Длина балки или плиты берется с необходимой глубиной опоры, которая берется из проекта. При разметке фундамента требуется предельная точность, ведь отклонение размеров приведет к расхождению вертикальных конструкций.

Горизонтальные элементы могут не вписываться в проектное положение или выпадать из монтажного пространства, поэтому потребуется пересчет длины и другие показатели.

Правильная разметка базы дает приятные бонусы при постройке здания:

строительство завода без отклонений от проекта.
соблюдение предусмотренной проектом экономии средств и материалов;
простота возведения стен и использования сборных элементов;

Перед тем, как измерить диагональ фундамента, необходимо выровнять строительную площадку, чтобы было удобно размечать линии на земле. Практически всегда конструкции и материалы зданий, от изоляционных матов до панелей и стеновых панелей, имеют прямые углы, поэтому фундамент также маркируется с учетом этих требований.

Определения и соглашения

Квадрат — это четырёхугольник с равными сторонами, все углы которого являются прямыми, то есть равны 90 градусов. Данная фигура одновременно и ромб, и прямоугольник, поэтому сохраняет все их свойства.
Диагональ многоугольника — это отрезок, соединяющий две его противоположные вершины. В статье её будем обозначать буквой d.
Противоположными называются вершины, не лежащие на одной стороне.
Корень квадратный из числа, это такое число, которое при умножении само на себя даст исходное. В геометрии используются только положительные значения квадратного корня. В статье его будем обозначать сокращением rad (от латинского radical — корень).
Сторону квадрата будем обозначать буквой a.

Как понятно из вышеизложенного, у квадрата только две диагонали. Поскольку квадрат является прямоугольником и сохраняет его свойства, то они равны между собой. Рассмотрим различные методы нахождения её длины.

Выравнивание величины прямоугольника

В прямоугольнике все углы должны быть 90 °, иначе получится неравнобедренная фигура с искаженными стенами. Контур фундамента имеет внешнюю и внутреннюю стороны, поэтому требование прямоугольности распространяется на оба контура. Проще всего выровнять значение для простого прямоугольного дома с четырьмя стенами.

Иногда фундамент в плане имеет сложную конструкцию, например, для пристройки или веранды делают дополнительные монолитные ленты, а каминный зал считается самостоятельным помещением. В этом случае разметка усложняется тем, что площадь дома будет состоять из отдельных прямоугольников, размеченных отдельно.

После планирования каждая фигура проверяется на соответствие остальным деталям, а также выставляются прямые углы между составляющими элементами. Исходная сторона прикреплена к основанию, что выглядит просто. Это может быть забор, забор, трамвайный путь или бордюр мощеного пути. Такое же расстояние проводится от этой линии, чтобы указать первую сторону желаемой плоскости фундамента.

После окончательной разметки необходимо правильно рассчитать диагональ и сравнить расстояние между первой-третьей и второй-четвертой вершинами прямоугольника на земле. У вас должны получиться абсолютно равные расстояния. Также проверяется длина противоположных сторон, которая также должна быть одинаковой.

Что такое площадь прямоугольника

Но для начала давайте все-таки дадим основные определения:

Прямоугольник – это геометрическая фигура, относящаяся к категории четырехугольников. Ее отличительная особенность в том, что противоположные стороны лежат на параллельных прямых (то есть параллельны друг другу) и равны.

А частным случаем прямоугольника, если у него все стороны равны между собой, является квадрат.

Площадь любой геометрической фигуры, формально говоря, это ее размер. Другими словами, размер того пространства, которое находится внутри границ фигуры.

В отношении четырехугольников применимо еще понятие « квадратура ». С его помощью показывали, сколько квадратов вместится внутрь фигуры.

Собственно, отсюда и пошло современное обозначение площадей, когда речь идет о габаритах помещения или какой-то территории. Мы часто слышим «столько-то квадратных метров (миллиметров, сантиметров, километров)» или просто «столько-то квадратов».

Для площади геометрических фигур действуют определенные правила :

Она не может быть отрицательной.
У равных фигур всегда равные площади.
Если две фигуры не пересекаются друг с другом, то их общая площадь равна сумме площадей фигур по отдельности.
Если одна фигура вписана в другую, то ее площадь всегда меньше, чем у второй.

» alt=»»>

Обычно фигуры, которые имеют равные площади, называют « равновеликими ».

Как вычислить периметр прямоугольника

Существует 2 способа его нахождения:

1 способ. Складываем все стороны. P = a + а + b + b
2 способ. Сложить ширину и длину, и умножить на 2. P = (a + b) · 2. ИЛИ Р = 2 · а + 2 · b. Стороны прямоугольника, которые лежат друг против друга (противолежащие), называются длиной и шириной.

«a» — длина прямоугольника, более длинная пара его сторон.

«b» — ширина прямоугольника, более короткая пара его сторон.

Пример задачи на подсчет периметра прямоугольника:

Вычислите периметр прямоугольника, есть его ширина равна 3 см., а длина — 6.

Полупериметр прямоугольника — когда выполняешь первое действие в скобках – (a+b).
Чтобы из полупериметра получить периметр, нужно его увеличить в 2 раза, т.е. умножить на 2.

Основные формулы для вычислений

Для изучения основных соотношений следует ввести некоторые обозначения, позволяющие избежать «тяжелых» записей, при которых обозначаются стороны и диагонали. Упрощенная форма имеет такой вид:

Прямоугольник: MNOP.
Стороны: MN = m и NО = n.
Диагональ (вводится одно обозначение, поскольку они равны): NP = t.
Периметр: Р.
Площадь: S.
Углы оснований: ∠М = ∠N = ∠O = ∠P = 90.
Радиус окружности: R.
Диаметр: D.
Углы при пересечении диагоналей: острый — ∠МТN = Q, тупой — ∠NTO = U.

На последний пункт следует обратить внимание, поскольку иногда молодые математики их путают, подставляя в формулу площади прямоугольника через диагонали.

Площадь и периметр фигуры

Периметр — сумма всех четырех сторон. Для его нахождения рекомендуется использовать соотношения:

S и одна из сторон: P = / m или P = / n.
t и m (n): P = 2m + 2(t 2 — a 2 )^(0.5)) = 2n + 2(t 2 — n 2 )^(0.5)).
m (n) и R: P = 2m + 2(4 * R 2 — m 2 )^(0.5)) = 2 * (n + (4 * R 2 — n 2 )^(0.5)).
m (n) и D: P = 2m + 2(D 2 — m 2 )^(0.5)) = 2n + 2(D 2 — n 2 )^(0.5)).

Для вычисления размерности прямоугольника используется понятие площади для двухмерной фигуры. Она измеряется в линейных единицах, возведенных в квадрат, т. е. мм 2 , см 2 , м 2 и т. д. Чтобы найти S, нужно воспользоваться соотношениями:

P и m (n): S =0.5 * = 0.5 * .
Две известные противоположные стороны: S = mn.
Площадь прямоугольника по диагонали t и m (n): S = m * ^(0.5) = n * ^(0.5).
Синус ∠МТN и t (формула площади через диагональ): S = 0.5 * .
R и m (n): S = m * ^(0.5) = n * ^(0.5).
Cторона и D: S = m * ^(0.5) = n * ^(0.5).

Найти площадь прямоугольника, зная диагональ и 2 стороны, поможет формула Нонаналя. Она имеет следующий вид: S = 2 * ^(1/2), где р = (m + n + t) / 2. Однако для решения задач будут также полезны и другие соотношения.

Другие полезные соотношения

При решении заданий иногда возникает необходимость найти не только P и S, но и другие параметры фигуры. Для этих целей рекомендуется использовать следующие соотношения:

m = ^(0.5) и n = ^(0.5).
m = S / n и n = S / m.
m = 0.5 * (P — 2 * n) и n = 0.5 * (P — 2 * m).
t = ^(0.5).
t = (S 2 + m 4 )^(0.5) / n= (S 2 + n 4 )^(0.5) / m.
sin(U) и m: R = m / 2sin (U).
cos(U) и n: R = n / 2cos (U).

Чтобы найти sin(U), нужно воспользоваться формулой: sin (U) = m / t, а cos (U) = n / t. Синус острого угла находится таким образом: sin (Q) = 2S / t 2 .

Как рассчитать площадь прямоугольника, если мы знаем только одну сторону и диагональ

Можно определить площадь прямоугольника другим способом. Формула, которая была изложена ранее, не является единственным методом, который можно использовать. Действительно, вполне возможно сделать это по-другому. Для этого нам нужно будет, по крайней мере, измерить только одну сторону и необходимо знать длину диагонали. В этом случае мы делаем расчет, используя теорему Пифагора.

Что такое теорема Пифагора

Это формула, которая используется для определения длины третьей стороны прямоугольного треугольника, когда вы уже знаете значение двух других его сторон.

Обратите внимание, что прямоугольник состоит из двух прямоугольных треугольников. Действительно, диагональ представляет гипотенузу этого типа треугольника

Теорема Пифагора

Кроме того, это также самая длинная сторона, которую можно найти на рисунке. Длина и ширина, с другой стороны, представляют две другие его стороны (скажем, смежные стороны). Это причина, почему можно использовать эту формулу для определения площади прямоугольника.

Теорема Пифагора основана на довольно простом уравнении, которое выглядит следующим образом: a² + b² = c². Где a и b используются для представления двух соседних сторон — катетов прямоугольного треугольника, а c представляет гипотенузу треугольника.

Чтобы полностью понять использование этой формулы, мы начнем с очень конкретного примера. Для этого предположим, что диагональ прямоугольника 10 см, а другая сторона 6 см. Если мы ссылаемся на формулу a² + b² = c², следовательно, сторона «a» составляет 6 см, а гипотенуза «c» — 10 см. Теперь нам нужно просто заменить буквенные значения числовыми значениями, которые у нас есть. Что дает нам:

a² + b² = c²
6² + b² = 10²
b² = 10² — 6²
b² = 100 — 36
b² = 64
b= 8
Мы получаем длину смежной стороны прямоугольника «b», которая равна 8 см. Теперь мы можем рассчитать площадь прямоугольника:

S = 8 см х 6 см
Следовательно, S = 48 см².

Чему равна площадь прямоугольника?

Умение рассчитывать площадь прямоугольника является базовым навыком для решения огромного количества бытовых или технических задач. Эти знания применяются практически во всех областях жизни! Например в тех случаях когда необходимы площади любых поверхностей в строительстве или недвижимости. При расчётах площадей земли, участков, стен домов, жилых помещений . не возможно назвать ни одной области деятельности человека, где это знание не может пригодиться!

Если расчёт площади прямоугольника вызывает у Вас сложности — просто воспользуйтесь нашим калькулятором! О моментально приведёт все необходимые вычисления и напишет текст решения с разъяснениями в деталях.

Принцип расчета площади прямоугольника

Чтобы вычислить площадь прямоугольника, мы посчитаем количество единиц областей, которые содержит прямоугольник:

В прямоугольнике выше 12 квадратов по 1 см². Его площадь составляет 12 см² (4 х 3).

Примечание. В этом расчете длина L и ширина l прямоугольника должны быть выражены в одной и той же единице длины. Результат будет выражен в той же единице измерения, возведенной в квадрат. Например, если длина прямоугольника выражена в метрах, ширина также должна быть выражена в метрах, а результат формулы для расчета площади прямоугольника даст результат в квадратных метрах (м²).

Площадь прямоугольника эквивалентна его территории. Территория — это термин, используемый для обозначения меры площади земли (мы используем единицу измерения гектар, а не м²). Гектар — это метрическая мера земельной площади, равная 10 000 м2.

Правильный расчет диагонали фундамента

Изучив основной план, нужно приступить к разметке одной из сторон. Это может быть боковая часть, передняя или задняя, в данном случае это не главное условие, потому что учитывается только ориентация направления.

Длина фундаментной стены не учитывается, можно от точки соседних углов отвести на 1,0 метр больше. В этих местах сажают жерди и натягивают шпагат. Приводится запас по длине, чтобы при рытье траншеи колышек не вырывался и оставался для обозначения направления борта.

Колышки заменяют на доску длиной 1-2 метра с прибитыми к концу колышками. Подключенный к ним кабель при необходимости можно быстро переставить из стороны в сторону. Такое приспособление для работы называется отливным, оно позволяет рисовать фактуру с точностью до нескольких миллиметров.

Порядок работы:

Перед вычислением диагонали прямоугольного треугольника по сторонам ставят 3 и 4 равные части, их размечают на проводе (например, 3 и 4 метра).
Проделайте то же самое с перпендикулярной стороной и определите направление.
Зависимость расстояния между отмеченными точками такова, что гипотенуза должна быть равна пяти частям (5 метров) и не отличаться ни на один сантиметр, иначе пойдет скос.
После натяжения шпагата находят ориентир по длине и определяют угол фундамента, в этой точке зацепляют за шпагат прищепку или в землю всаживают кол, затем появляются 2 угла.

Формулы прямоугольника:

Пусть a – длина прямоугольника, b – ширина прямоугольника, d – диагональ и диаметр описанной окружности прямоугольника, R – радиус описанной окружности прямоугольника, P – периметр прямоугольника, S – площадь прямоугольника.

Формула стороны прямоугольника (длины и ширины прямоугольника):

Формула диагонали прямоугольника:

d = 2R.

Формулы периметра прямоугольника:

P = 2a + 2b,

P = 2(a + b).

Формулы площади прямоугольника:

S = a · b.

Формула радиуса окружности, описанной вокруг прямоугольника:

Примечание: Фото https://www.pexels.com, https://pixabay.com

Видео https://www.youtube.com/watch?v=_EVDcbOydAI

Найти что-нибудь еще?

карта сайта

Коэффициент востребованности
2 688

Необходимые инструменты для работы

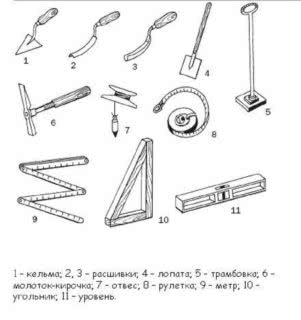
Инструменты для разметки фундамента

При рытье траншей экскаватором снимают канаты, которые протягивают с углов, а точки сторон размечают на земле присыпкой контрастным веществом, например светлым песком или мелом. Элементы ветоши окрашены яркой краской, чтобы экскаватор мог их видеть и не наезжать на маркировочные детали. После рытья траншеи веревки натягиваются на старое место и проверяется положение ям или канав.

Расчет диагонали фундамента проводится с помощью инструментов и приспособлений:

угольник, рулетка, молоток, ножницы;
прочный нейлоновый шнур или шпагат;
гвозди, шурупы или шурупы;
отвес, водяной или лазерный уровень.
колышки деревянные или даже арматура, без кривизны;
также отрезки металлического профиля или сухой полосы по 2 – 2,5 метра для горизонтального переноса точек;

Геодезисты используют теодолит, чтобы отмечать углы и высоту. У частных трейдеров такого инструмента нет; для работы с ним требуется умение. Правильно измерить диагональ дома можно простыми приборами.

На угольник закреплены лазерные указки и строительный уровень – такой прибор покажет высокую точность разметки. Продаются транспортиры и квадраты большого размера, лучше брать, чтобы удобнее было переносить линии плоскости на землю. Первоначальные отметки очень важны для начала строительства, поэтому желательно несколько раз рассчитать диагональ, чтобы убедиться, что она работает правильно.

Как выбрать оптимальную диагональ телевизора?

Диагональ экрана телевизора – относительно самостоятельная характеристика, не зависящая от других параметров устройства. Современный электронный рынок – прямое тому подтверждение. Так, например, сегодня можно легко найти модели с относительно небольшой диагональю и высоким разрешением или, наоборот, с низким разрешением и большой диагональю. Однако этот факт не означает, что при выборе новой ТВ-панели нужно ориентироваться исключительно на размер дисплея. Комфортность просмотра, качество изображения и детализация зависят от соотношения диагонали, разрешения и сторон монитора.

Для выбора оптимальной модели телевизора рекомендуем придерживаться следующих правил:

Чем больше диагональ телевизора, тем выше должно быть разрешение экрана. Дело в том, что на больших телевизионных панелях легко можно увидеть любые изъяны и изъяны отображаемого изображения.
Чем меньше соотношение сторон, тем меньше диагональ экрана. В случае, если речь идет об огромном телевизоре с соотношением сторон 4: 3, большая площадь монитора будет «съедена» черными кадрами
Чем больше комната, тем больше диагональ и наоборот, чем меньше комната, тем меньше диагональ. Вот простое правило. Так, например, если речь идет о маленькой кухне, оптимальным вариантом будет компактный 19-22-дюймовый монитор

Если покупатель планирует оборудовать полноценный домашний кинотеатр в большой гостиной, есть смысл обратить внимание на современные жидкокристаллические панели с диагональю от 90 дюймов и более.

Для стандартных комнат площадью 16-20 квадратов оптимальным параметром экрана будет 32-40 дюймов с соотношением сторон 16: 9 и разрешением 1920 * 1080. Если монитор меньше, зрители их не увидят сможете в полной мере насладиться резкостью и качеством изображения. Если вы купите телевизор размером более 40 дюймов, глаза тех, кто находится в комнате, начнут уставать в течение 40-60 минут после просмотра любимого фильма

В любом случае, выбирая оптимальную диагональ телевизора, в первую очередь нужно обращать внимание на свои вкусы, потребности, иначе дорогая покупка не принесет радости

Сложности при неправильной разметке

Нарушение геометрии фундамента снижает прочность стен

Неправильный перенос размеров на землю и отказ от сравнения диагоналей приведет к появлению на поверхности земли ромба или трапеции. При возведении самого фундамента это может не стать заметным, но первая кладка плит над цоколем выявит несоответствия и приведет к пустой трате времени на пересчет сборных элементов или переделку основания.

Если плита размещена на глубине меньше необходимой, после загрузки оборудованием или людьми она может сломаться в несущей части стены и упасть. Это раздражение затронет горизонтальные элементы пола на всех этажах небоскреба и будет повторяться вплоть до крыши.

устройство кровли выполнить сложно, если размеры между стропилами не совпадают, фермы нужно устанавливать в большем размере и в других местах уменьшать размер. Сложность работы возрастает, ведь исполнитель играет необычную роль дизайнера и дизайнера.

Монтаж кровли усложнится, ведь доступны листы гофрокартона или шифера с прямым углом. Сборные угловые водосточные элементы также рассчитаны на установку под углом 90 °, карниз отойдёт от края крыши и вода будет падать на вертикальные ограждения, стены будут увлажнены.

Типовые примеры

Для решения задач на нахождение катета не нужно обладать какими-то особенными знаниями. Нужно просто внимательно проанализировать условие. Например, пусть известно, что в прямоугольнике один катет длиннее другого на пять сантиметров. При этом площадь фигуры равняется 84 сантиметрам в квадрате. Необходимо определить длины сторон и периметр.

Так как в условии дана площадь, то при решении необходимо отталкиваться от неё. Известно, что площадь прямоугольного треугольника находится по формуле: S = AC*CB/2. Это выражение является частным случаем общей формулы для нахождения площади любого треугольника, где: AC — это высота, а CB — основание. Если принять, что AC равно X, то, согласно условию, длина CB будет составлять x+5.

Исходя из этого, площадь треугольника будет равна: S = (x*(x+5))/2. Подставив вместо S заданное значение, можно получить квадратное уравнение: x2 + 5x — 84 = 0. Решать его лучше методом детерминанта. Корнями уравнения будут -12 и 7. Так как -12 не удовлетворяет условию задачи, то верным ответом будет семь.

Длина второго катета равняется семи сантиметрам. Первого: AC = 7−5 = 2 см. Зная оба катета, по теореме Пифагора можно найти гипотенузу: c = (22 + 72)½ = (4+49)½ = 531/2 = 7,3 см. Найдя длины всех сторон, можно без усилий найти периметр обыкновенным сложением: P = 2+7+7,3 = 16,3 см. Задача решена.

Довольно интересные, но в то же время простые задачи на нахождение сторон и углов при известной длине гипотенузы и значения разворота одной из вершин. Пусть имеется прямоугольный треугольник, у которого гипотенуза BC равняется пяти сантиметрам, а угол между ней и катетом составляет 60 градусов. Нужно определить все остальные стороны и углы.

Так как известна гипотенуза и острый угол, то, воспользовавшись тригонометрическими формулами, можно найти длины катетов: AC=BC*sin60 = 5*(3)½/2; AB=BC*cos60 = 5/2. Сумма всех углов в треугольнике равна 180 градусов, так как один из них прямой, а второй задан и составляет 60 градусов, то третий находится путём вычитания C = 180 — (90 + 60) = 30.

Общая информация

В задачах с физико-математическим уклоном нужно вычислять некоторые параметры прямоугольника: размерность углов, длины сторон и диагоналей, величину периметра и площади. Они связаны между собой математическими соотношениями.

Методику расчета должен знать каждый, поскольку величины применяются не только в решении заданий, но и при ремонте. Например, следует рассчитать количество плитки для пола в ванной, которая имеет форму прямоугольника. Если воспользоваться свойством диагоналей, можно выяснить, каким методом следует ее укладывать на пол.

Чтобы воспользоваться конкретным соотношением для определенной фигуры, ее сначала нужно идентифицировать для правильного применения расчетной формулы. При неверном определении прямоугольника вычисления будут недостоверными, что негативно скажется на зачетности по физико-математическим дисциплинам или закупке материалов для выполнения ремонтных работ.

Основные понятия

Прямоугольник – это четырехугольник, у которого все углы прямые, а противоположные стороны попарно равны и параллельны. В нашей жизни многие фигуры имеют форму прямоугольника. Например, поверхность стола, тетрадь и другие.

Рассмотрим пример:по границам земельного участка необходимо поставить забор. Для того чтобы узнать длину каждой из сторон необходимо их измерить.

Рис. 1. Земельный участок формой прямоугольника.

Земельный участок имеет стороны длиной 2 м, 4 м, 2 м, 4 м. Поэтому чтобы узнать общую длину забора необходимо сложить длины всех его сторон:

2+2+4+4= 2·2+4·2 =(2+4)·2 =12 м.

Именно эта величина в общем случае и называется периметром. Таким образом, для нахождения периметра необходимо сложить все стороны фигуры. Для обозначения периметра используют латинскую букву P.

Для вычисления периметра произвольной фигуры не нужно разделять её на прямоугольники, нужно измерить линейкой (рулеткой) лишь все стороны данной фигуры и найти их сумму.

Периметр прямоугольника измеряется в различных единицах длины: мм, см, м, км и так далее. При необходимости, данные в задании, переводят в одинаковые единицы измерения.

Как перевести дюймы в сантиметры

С одной стороны, как мы видим, вы можете измерить диагональ телевизора с помощью обычной рулетки. Однако, с другой стороны, следует учитывать разницу в единицах измерения – сантиметрах и дюймах. Конечно, при желании можно найти линейку со шкалой, которая без лишних вычислений покажет желаемый результат. Но поскольку в нашей стране официально используется метрическая система измерения, найти дюймовую линейку или рулетку будет очень сложно. Единственный выход в этой ситуации – перевести сантиметры в дюймы или наоборот с помощью обычного или онлайн-калькулятора.

По сути, все, что нужно для решения такой проблемы, – это знать, что 1 дюйм равен 2,54 сантиметра. Тем, чтобы получить ответ на вопрос, как рассчитать диагональ телевизора, нужно произвести замеры с помощью стандартной рулетки, после чего результат разделить на 2,54, округлив частное.

Например. С помощью рулетки мы выяснили, что диагональ экрана телевизора составляет 82 сантиметра. Разделите 82 на 2,54, чтобы получить 32,28. Следовательно, необходимая диагональ ТВ панели – 32 дюйма.

Для тех, кто не хочет рассчитывать параметры вручную, мы подготовили таблицу для перевода сантиметров в дюймы и наоборот.

Таблица сравнения диагоналей

Дюймы	Сантиметры
22	60
32	82
37	94
40	102
42	107
50	127
60	152
70	178
100	254

Используя эту таблицу, вы можете быстро преобразовать сантиметры в дюймы и наоборот, рассчитав таким образом диагональ телевизора с помощью обычной рулетки.

Формула площади прямоугольника — посчитать!

L * H = S чтобы найти площадь прямоугольника, необходимо перемножить ширину на длину. Другими словами её можно выразить так: площадь прямоугольника равна произведению сторон.

1. Приведём пример расчёта как найти площадь прямоугольника, стороны равны известным величинам, например ширина 4 см, длина 8 см.

Как найти площадь прямоугольника со сторонами 4 и 8 см: Решение простое! 4 х 8 = 32 см2. Чтобы решить такую простую задачу нужно вычислить произведение сторон прямоугольника или просто умножить ширину на длину, это и будет площадь!

2. Частным случаем прямоугольника является квадрат, это тот случай когда стороны у прямоугольника равны, в этом случае найти площадь квадрата можно по выше приведённой формуле.

Площадь сложных фигур

Площадь всей фигуры равна сумме площадей её частей.

Задача: найти площадь огородного участка.

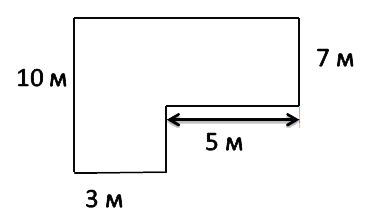
Так как фигура на рисунке не является ни квадратом, ни прямоугольником, рассчитать её площадь можно используя правило выше.

Разделим фигуру на два прямоугольника, чьи площади мы можем легко рассчитать по известной формуле.

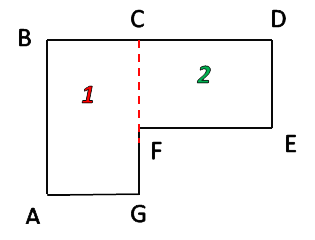S_ABCE = AB · BC S_EFKL = 10 · 3 = 30 м 2 S_CDEF = FC · CD S_CDEF = 7 · 5 = 35 м 2

Чтобы найти площадь всей фигуры, сложим площади найденных прямоугольников. S = S_ABCE + S_EFKLS = 30 + 35 = 65 м 2

Ответ: S = 65 м 2 — площадь огородного участка.

Свойство ниже может вам пригодиться при решении задач на площадь.

Диагональ прямоугольника делит прямоугольник на два равных треугольника.

Площадь любого из этих треугольников равна половине площади прямоугольника.

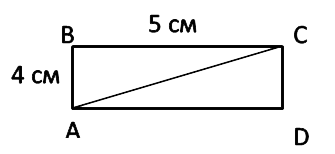
АС — диагональ прямоугольника ABCD . Найдём площадь треугольников ABC и ACD

Вначале найдём площадь прямоугольника по формуле.

S_ABCD = AB · BC S_ABCD = 5 · 4 = 20 см 2

S_ABC = S_ABCD : 2

S_ABC = 20 : 2 = 10 см 2

S_ABC = S_ACD = 10 см 2

Чему равна площадь прямоугольника? 1. Необходимо знать длину и ширину прямоугольника. 2. Внесите значения сторон в графы ниже. 3. Нажмите кнопку рассчитать площадь прямоугольника!

Что такое прямоугольник

Давайте не будем «срезать углы». Чтобы иметь возможность вычислить площадь прямоугольника, естественно, что мы сначала знаем, что это такое. Поэтому для начала необходимо помнить, что прямоугольник является четырехугольником. Другими словами, это геометрическая фигура, которая имеет четыре стороны и четыре прямых угла. Противоположные стороны прямоугольника имеют одинаковую длину. Две самые длинные стороны представляют его длину, а две другие стороны представляют его ширину.

Не все четырехугольники являются прямоугольниками. Действительно, обязательно, чтобы они имели следующие свойства, чтобы мы могли сказать, что это действительно прямоугольник:

Что такое прямоугольник

Определение

Прямоугольник — параллелограмм, в котором все углы прямые.

В евклидовой геометрии для того, чтобы четырёхугольник был прямоугольником, достаточно, чтобы хотя бы три его угла были прямые, тогда четвёртый угол в силу теоремы о сумме углов многоугольника также будет равен 90°.

Свойства

Противоположные стороны попарно равны.
Диагонали равны. Они пересекаются и точкой пересечения делятся пополам.
Биссектриса отсекает от прямоугольника равнобедренный треугольник.
Стороны прямоугольника являются его высотами.
Квадрат диагонали прямоугольника равен сумме квадратов двух его соседних сторон.
Около любого прямоугольника можно описать окружность, при этом ее диаметр численно равен диагонали прямоугольника.

Признаки

Параллелограмм является прямоугольником при выполнении одного из следующих условий:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут

Диагонали параллелограмма равны.
Сумма квадратов соседних сторон параллелограмма равна квадрату диагонали.
Все углы параллелограмма равны.

Вычисление по радиусу описанной и вписанной окружности

Ещё один способ, который на само деле очень простой. Радиус описанной окружности будем обозначать латинской буквой R, радиус вписанной окружности будем обозначать латинской буквой r.

Сначала разберёмся с описанной окружностью. В данной ситуации её радиус составляет ровно половину диагонали (это нетрудно убедиться с использованием построения), таким образом: R = 1/2*d. отсюда имеем: d = два*R. Снова поясним наши рассуждения на примере. Пусть R = 45 километров. Получим, d = два*45 = 90 километров.

И, наконец, рассмотрим метод, связанный с радиусом вписанной окружности. Опять-таки из построения чётко видно, что диаметр вписанной окружности равняется стороне квадрата. Таким образом, её радиус вдвое меньше стороны. Запишем это в виде формулы: r = 1/2*a. Отсюда следует, a = 2*r. Снова воспользуемся формулой из первого метода, подставим вместо стороны её выражение через радиус вписанной окружности. Выражение примет вид: d = rad2*a = rad2*2*r.

Ещё раз воспользуемся помощью примера. Пусть r = 98 метров. Тогда имеем, d = rad2*2*98 = 196*rad2.

Заключение

Внимательно изучив все вышеизложенное, можно сделать вывод — определение площади произвольного четырёхугольника с разными сторонами сложнее, чем у них же специальных видов — квадрата, прямоугольника, ромба, трапеции, параллелограмма. Однако внимательно изучив все приведённые методы, можно с лёгкостью решать задачи необходимые для школьников. Сведём все наши формулы в одну таблицу:

S = 1/2*d1*d2*sin(d1,d2);
S = rad(( p − a )*( p − b )*( p − c )*( p − d ) − a*b*c*d*c o s^2( (a,b) + (c,d))/2), где p = 1/2*(a + b + c + d);
S = ((a + b+ c + d)/2)*r

S = rad((p − a )*( p − b )*( p − c )*( p − d ), где p равно половине периметра.

Таким образом, реально сложной является только формула номер 2, но и она вполне доступна, при условии хорошего понимания данных в статье определений и соглашений.

Заключение

Таким образом, мы рассмотрели в статье пять принципиально различных методов вычисления диагонали квадрата. Если, на первый взгляд, задача казалась сложной, то после проведённых нами рассуждений стало очевидно, что особых проблем здесь нет. Сведём все полученные нами формулы в одну таблицу.

d = rad2*a;
d = rad2*radS;
d = rad2*P/4;
d = 2*R;
d = rad2*2*r.

Хочется ещё отметить, что с помощью первой из наших формул очень легко построить отрезок, равный корню квадратному из двух. Для этого строим квадрат со стороной единица, его диагональ и будет равняться искомому отрезку.

Если на полученной диагонали мы построим прямоугольник, используя её как длину, а ширину возьмём равной единице, то получим отрезок равный ещё одному иррациональному числу корень квадратный из трёх.

Продолжая нашу цепочку и далее, мы научимся строить отрезки равные любому иррациональному числу.

Площадь прямоугольника онлайн