Содержание:
Острый, тупой, равнобедренный, равносторонний… Когда дело доходит до треугольников, существует много различных разновидностей, но лишь немногие из них являются «особенными». У этих специальных треугольников есть стороны и углы, которые согласованы и предсказуемы, и их можно использовать, чтобы сократить ваш путь через геометрические или тригонометрические задачи. И треугольник 30-60-90, произносимый как «тридцать шестьдесят девяносто», действительно оказывается совершенно особенным типом треугольника.
В этом руководстве мы расскажем, что такое треугольник 30-60-90, почему он работает и когда (и как) использовать свои знания о нем. Итак, приступим!
Как найти равные катеты, при известной гипотенузе
- гипотенуза (обозначим ее буквой «c») равна х см: c=x;
- первый катет (обозначим его буквой «a») равен второму катету ((обозначим его буквой «b»): a=b;
В этом варианте решение задачи основывается на использовании теоремы Пифагора. Ее применяют к прямоугольным треугольникам и основной ее вариант звучит, как: «Квадрат гипотенузы равен сумме квадратов катетов». Так, как катеты у нас равны, то мы можем обозначать оба катета одним и тем же сиволом: a=b, значит — a=a.
- Подставляем наши условные обозначения в теорему (с учетом вышеизложенного): c^2=a^2+a^2,
- Далее максимально упрощаем формулу: с^2=2*(a^2) — группируем, с=√2*а — подносим обе части уравнения к квадратному кореню, a=c/√2 — выносим искомое.
- Подставлем данное значение гипотенузы и получаем решение: a=x/√2
Почему это работает: 30-60-90 Доказательство теоремы о треугольнике
Но почему этот особый треугольник работает именно так? Как мы узнаем, что эти правила законны? Давайте подробно рассмотрим, как работает теорема о треугольнике 30-60-90, и докажем, почему эти длины сторон всегда будут согласованными.
Во-первых, давайте на секунду забудем о прямоугольных треугольниках и посмотрим на равносторонний треугольник.
Равносторонний треугольник — это треугольник, у которого все стороны и углы равны. Поскольку внутренние углы треугольника всегда составляют в сумме 180 °, а $ 180/3 = 60 $, равносторонний треугольник всегда будет иметь три угла по 60 °.
Теперь давайте снизим высоту от самого верхнего угла до основания треугольника.
Мы сейчас создал два прямых угла и два равных (равных) треугольника.
Откуда мы знаем, что это равные треугольники? Потому что мы упали с высоты равносторонний треугольник, основание мы разделили ровно пополам. Новые треугольники также имеют одну длину стороны (высоту), и каждый из них имеет одинаковую длину гипотенузы. Поскольку они имеют три общих длины стороны (SSS), это означает треугольники равны.
Примечание: два треугольника конгруэнтны на основе принципов длины стороны-стороны-стороны или SSS, но также основаны на измерениях стороны-угла-стороны (SAS), угла-угла-стороны (AAS) и угла-стороны. боковой угол (ASA). По сути? Они определенно совпадают.
Теперь, когда мы доказали конгруэнтность двух новых треугольников, мы видим, что каждый из верхних углов должен быть равен 30 градусам (потому что каждый треугольник уже имеет углы 90 ° и 60 ° и в сумме должно составлять 180 °). Это означает мы сделали два треугольника 30-60-90.
И поскольку мы знаем, что мы разрезаем основание равностороннего треугольника пополам, мы можем видеть, что сторона, противоположная углу 30 ° (самая короткая сторона) каждого из наших треугольников 30-60-90, составляет ровно половину длины гипотенузы. .
Итак, давайте назовем нашу исходную длину стороны $ x $ и нашу длину, разделенную пополам, $ x / 2 $.
Теперь все, что нам остается сделать, это найти длину средней стороны, которую разделяют два треугольника. Для этого мы можем просто использовать теорему Пифагора.
$ а ^ 2 + Ь ^ 2 = с ^ 2 $
$ (х / 2) ^ 2 + Ь ^ 2 = х ^ 2 $
$ b ^ 2 = x ^ 2 — ({x ^ 2} / 4) $
$ b ^ 2 = {4x ^ 2} / 4 — {x ^ 2} / 4 $
$ b ^ 2 = {3x ^ 2} / 4 $
$ b = {√3x} / 2 $
Итак, у нас осталось: $ x / 2, {x√3} / 2, x $
Теперь давайте умножим каждую меру на 2, чтобы облегчить жизнь и избежать использования дробей. Таким образом, у нас останется:
$ x $, $ x√3 $, $ 2x $
Таким образом, мы видим, что треугольник 30-60-90 будет всегда имеют согласованные длины сторон $ x $, $ x√3 $ и $ 2x $ (или $ x / 2 $, $ {√3x} / 2 $ и $ x $).
К счастью для нас, мы можем доказать, что правила треугольника 30-60-90 верны без всего … этого.
Табличные значения sin 30, cos 30 и tg 30 градусов:
Якорь: #sin30 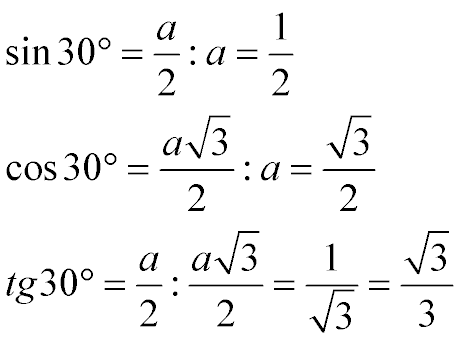
То есть:
Тангенс 30 градусов равен корню из трех на три
Синус 30 градусов равен одной второй или 0,5
Косинус 30 градусов равен корню из трех на два
|
Исходя из написанного выше принципа перевода радиан в градусы, угол пи на 6 будет равен
Для более удобного визуального восприятия эти значения приведены ниже на рисунке |
Синус, косинус і тангенс кута пі на 6 (π/6) Виходячи з написаного вище принципу переведення радіан в градуси, кут пі на 6 дорівнюватиме
Для зручнішого візуального сприйняття ці значення приведені нижче на малюнку |
Синус, ко синус, тангенс угла 15 градусов (sin 15 cos 15 tg 15)Описание курса Синус, косинус, тангенс угла 45 градусов (sin 45, cos 45, tg 45)
Формулы и свойства прямоугольного треугольника
Обозначения формул:
(см. рисунок выше)
a, b — катеты прямоугольного треугольника
c — гипотенуза
α, β — острые углы треугольника
S — площадь
h — высота, опущенная из вершины прямого угла на гипотенузу
ma— медиана, проведенная к стороне a из противолежащего угла (α)
mb — медиана, проведенная к стороне b из противолежащего угла (β)
mc — медиана, проведенная к стороне c из противолежащего угла (γ)
В прямоугольном треугольнике любой из катетов меньше гипотенузы (Формулы 1 и 2). Данное свойство является следствием теоремы Пифагора.
Косинус любого из острых углов меньше единицы (Формулы 3 и 4). Данное свойство следует из предыдущего. Так как любой из катетов меньше гипотенузы, то из соотношение катета к гипотенузе всегда меньше единицы.
Квадрат гипотенузы равен сумме квадратов катетов (теорема Пифагора). (Формула 5). Это свойство постоянно используется при решении задач.
Площадь прямоугольного треугольника равна половине произведения катетов (Формула 6)
Сумма квадратов медиан к катетам, равна пяти квадратам медианы к гипотенузе и пяти квадратам гипотенузы, деленных на четыре (Формула 7). Кроме указанной, есть еще 5 формул, поэтому рекомендуется ознакомиться также и с уроком «Медиана прямоугольного треугольника», в котором более подробно изложены свойства медианы.
Высота прямоугольного треугольника равна произведению катетов, деленному на гипотенузу (Формула 8)
Квадраты катетов обратно пропорциональны квадрату высоты, опущенной на гипотенузу (Формула 9). Данное тождество также является одним из следствий теоремы Пифагора.
Длина гипотенузы равна диаметру (двум радиусам) описанной окружности (Формула 10). Гипотенуза прямоугольного треугольника является диаметром описанной окружности. Это свойство часто используется при решении задач.
Радиус вписанной в прямоугольный треугольник окружности можно найти как половину от выражения, включающего в себя сумму катетов этого треугольника минус длину гипотенузы. Или как произведение катетов, деленное на сумму всех сторон (периметр) данного треугольника. (Формула 11) Синус угла А (α, альфа) в прямоугольном треугольнике будет равен отношению противолежащего данному углу катета к гипотенузе (по определению синуса). (Формула 12). Данное свойство используется при решении задач. Зная величины сторон, можно найти угол, который они образуют.
Косинус угла А (α, альфа) в прямоугольном треугольнике будет равен отношению прилежащего данному углу катета к гипотенузе (по определению синуса). (Формула 13)
См. также Соотношения между углами и сторонами прямоугольного треугольника изучает Тригонометрия.
Содержание главы:
Прямоугольный треугольник
Биссектриса в прямоугольном треугольнике
Высота в прямоугольном треугольнике
Высота в прямоугольном треугольнике (Часть 2)
Теорема Пифагора и ее доказательство
Применение теоремы Пифагора
Гипотенуза прямоугольного треугольника
Перпендикуляр к плоскости прямоугольного треугольника
Подобие треугольников. Использование в задачахОписание курса Прямоугольный треугольник
Признаки равенства прямоугольных треугольников
Существует 4 признака равенства прямоугольных треугольников:
- Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны.
- Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и острому углу другого прямоугольного треугольника, то такие треугольники равны.
- Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.
- Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны.
Чтобы быстрее запомнить данные признаки, можно использовать их краткую трактовку:
- по катетам;
- по катету и прилежащему острому углу;
- по гипотенузе и острому углу;
- по гипотенузе и катету.
Как были вычислены значения синуса, косинуса и тангенса 30 градусов?
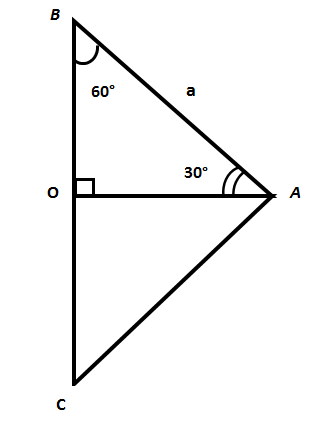
Значения тригонометрических функций синуса, косинуса, тангенса при α=30°Рассмотрим равносторонний треугольник АВС. Пусть, каждая из его сторон будет равна a. Согласно свойствам равностороннего треугольника, все его углы равны, в том числе угол ∠В=60°. Значения синуса, косинуса и тангенса мы можем вычислить, если найдем соотношение соответствующих сторон для угла 30 градусов в прямоугольном треугольнике. Так как значение этих тригонометрических функций зависит исключительно от градусной меры угла, то вычисленные нами соотношения и будут значениями синуса 30, косинуса 30 и тангенса 30 градусов. Сначала совершим дополнительные построения. Из вершины А на сторону BC проведем медиану AO. Медиана АО в равностороннем треугольнике одновременно является биссектрисой и высотой. Тогда треугольник АОВ – прямоугольный с углом ∠ВАО=30°. (Угол В равен 60 градусам, ∠ВOA прямой и равен 90 градусам, следовательно, ∠ВАО = 180 — 90 — 60 = 30 градусов) |
Значення тригонометричних функцій синуса, косинуса, тангенса при α=30°Розглянемо рiвнобiчний трикутник АВС. Хай, кожна з його сторін буде рівна а. Згідно з властивостями рівностороннього трикутника, всі його кути рівні, у тому числі кут ∠В=60°. Значення синуса, косинуса і тангенса ми можемо обчислити, якщо знайдемо співвідношення відповідних сторін для кута 30 градусів в прямокутному трикутнику. Оскільки значення цих тригонометричних функцій залежить виключно від градусної міри кута, то обчислені нами співвідношення і будуть значеннями синуса 30, косинуса 30 і тангенса 30 градусів. Спочатку зробимо додаткові побудови. З вершини А на сторону BC проведемо медіану АO. Медіана АО у рівносторонньому трикутнику одночасно є бісектрисою і висотою. Тоді тикутник АОВ — прямокутний з кутом ∠ВАО=30°. (Кут В дорівнює 60 градусам ∠ВOA прямій і дорівнює 90 градусам, отже ∠ВАО = 180 — 90 — 60 = 30 градусів) |
|
Для полученного прямоугольного треугольника вычислим значения тригонометрических функций его углов. Сделаем это сначала для угла 30 градусов. Величина гипотенузы нам известна и равна a. Катет OB равен a/2 , так как AO — медиана треугольника ABC. Найдем катет AO. По теореме Пифагора: АВ2=АО2+ОВ2; АО2=АВ2-ОВ2 подставим в полученное выражение значение гипотенузы (мы приняли, что оно равно а) АО2=a2- (а/2)2 АО2=3a2/4 AO=√( 3a2/4 ) =a√3/2 Теперь мы вычислили все стороны прямоугольного треугольника ABO. Учитывая, что AB = a, OB = a/2, AO = a√3/2, из соотношений сторон прямоугольного треугольника рассчитаем полученные значения. Согласно определению синуса, косинуса и тангенса: sin 30 = OB / AB (по определению синуса — отношение противолежащего катета к гипотенузе) cos 30 = AO / AB (по определению косинуса — отношение прилежащего катета к гипотенузе) tg 30 = OB / AO (по определению тангенса — отношение противолежащего катета к прилежащему) Откуда: Так как треугольник ABC — равносторонний, то BO равно AB/2, а значение AO вычислено выше. В результате получаем табличные значения sin 30, cos 30 и tg 30 градусов |
Для отриманого прямокутного трикутника обчислимо значення тригонометричних функцій його кутів. Зробимо це спочатку для кута 30 градусів. Величина гіпотенузи нам відома і рівна а. Катет OB рівний a/2, оскільки АO — медіана трикутника ABC. Знайдемо катет АТ. По теоремі Піфагора: АВ2=АО2+ОВ2; АО2=АВ2-ОВ2 пiдставимо в одержане рiвняння значення гiпотенузи (намi прийнято, що воно равно а) АО2=a2- (а/2)2 АО2=3a2/4 AO=√( 3a2/4 ) =a√3/2 Тепер ми обчислили всі сторони прямокутного трикутника ABO. Враховуючи, що AB = a, OB = a/2, AO = a√3/2, iз спiввiдношень сторiн прямокутного трикутника розрахуємо одержанi значення. Згiдно визначенню сiнуса, косiнуса та тангенса: sin 30 = OB / AB (за визначенням синуса — відношення катета, що протилежить, до гіпотенузи) cos 30 = AO / AB (за визначенням косинуса — відношення прилеглого катета до гіпотенузи) tg 30 = OB / AO (за визначенням тангенса — відношення катета, що протилежить, до прилеглого) Звiдки маємо: Враховуючи, що трикутник ABC — рiвнобiчний, то BO равно AB/2, а значення AO розраховано вище. В результатi одержуємо табличнi значення sin 30, cos 30 и tg 30 градусiв |
Градусы драматические: косинус 90 градусов равен нулю
А что как напряжение и ток отклоняются друг от друга на 90 градусов?! Ведь косинус такого угла равен нулю. Умножение на ноль есть ноль. Это, что называется, страшный сон энергетиков – ужасная апокалиптическая драма!
Представьте себе, газ сжигается на тепловых электростанциях, вода крутит турбины на гидроэлектростанциях, нейтроны делятся в реакторах атомных электростанций. Ток «бежит» по проводам в дома. А там – косинус угла «фи» равен нулю – полный швах! Батареи не греют, лампочки не светятся, холодильники не работают.
Чтобы мысленный эксперимент с отклонением напряжения и тока на 90 градусов не стал реальностью, энергетики по всему миру постоянно следят за «косинусом фи». Денно и нощно, без устали, без перерывов.
Почему отклоняются напряжение и ток? Из-за потребителей электричества! Нет, не из-за домашних электрических обогревателей. И не из-за домашних лампочек накаливания. Но из-за оборудования заводов и фабрик.
Везде, где крутятся электромоторы, их «кручение» приводит как бы к обратному закручиванию электричества. Работающее оборудование возвращает энергетикам в электрические сети сдвинутое между собой напряжение и ток.
Образно говоря, чтобы крутить моторы, электричество должно «упираться» во что-то. И из-за этого понемногу «проворачивается» в обратную сторону. Что и приводит к возникновению угла сдвига между напряжением и током.
Если не следить за последствиями такого «сдвига», то угол между напряжением и током будет постоянно расти. Косинус фи начнет уменьшаться. Электростанции начнут работать сначала чуть-чуть вхолостую, потом все больше и больше, потом еще больше…
Пример 5: Поиск недостающих сторон для одной стороны треугольника 30-60-90
Используйте рисунок ниже, чтобы вычислить меру недостающих сторон треугольника 30-60-90.
- Если c = 10, найдите a и b.
- Если b = 11, найдите a и c.
- Если a = 6, найдите b и c.
Нахождение недостающих сторон на одной стороне треугольника 30-60-90
Джон Рэй Куэвас
Решение
Обратите внимание, что данное c — гипотенуза треугольника. Используя формулы быстрого доступа, найдите a и b
а = с / 2
а = 10/2
а = 5 единиц
Ь = (с / 2) (√3)
б = (10/2) (√3)
b = 5√3 единиц
Обратите внимание, что данное b является более длинным участком треугольника 30-60-90. Используя формулы паттернов, найдите a и c
Рационализируйте полученное значение, чтобы получить точную форму.
а = Ь / (√3)
a = 11 / √3 единиц
с = (2 / √3) (б)
с = (2 / √3) (11)
с = 22 / √3
c = (22√3) / 3 единицы
Данное значение представляет собой более короткий отрезок треугольника 30-60-90. Используя теорему о треугольнике 30-60-90, найдите значения b и c.
б = √3 (а)
b = 6√3 единиц
c = 2a
с = 2 (6)
c = 12 единиц
Окончательный ответ
- a = 5 единиц и b = 5√3 единиц
- a = 11√3 единиц и c = (22√3) / 3 единицы
- b = 6√3 единиц и c = 12 единиц
Формулы прямоугольного треугольника:
Пусть a и b – длины катетов прямоугольного треугольника, с – длина гипотенузы прямоугольного треугольника, h – высота прямоугольного треугольника, проведенная к гипотенузе (АН), R – радиус описанной окружности, r – радиус вписанной окружности (см. Рис. 9, 11, 12).
Формулы сторон прямоугольного треугольника (a, b, c) по теореме Пифагора:
c2 = a2 + b2 ,
a2 = c2 – b2 ,
b2 = c2 – a2 .
Формула радиуса вписанной окружности (r):
.
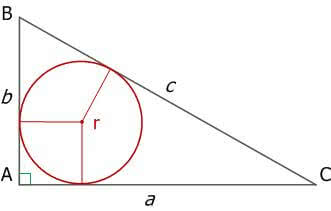
Рис. 12. Прямоугольный треугольник и вписанная окружность
Формула радиуса описанной окружности (R):
.
Формулы площади (S) прямоугольного треугольника:
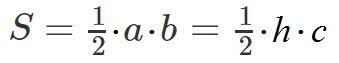 .
.
Формулы высоты (h)прямоугольного треугольника:
.
Примечание: Фото https://www.pexels.com, https://pixabay.com
Найти что-нибудь еще?
карта сайта
Коэффициент востребованности
18 641
Теорема Пифагора
Древнегреческий философ, ученый, математик – Пифагор Самосский вывел теорему, которая до сих применима для решения задач. Теорема названа в честь него – «теорема Пифагора».
Трактовка
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
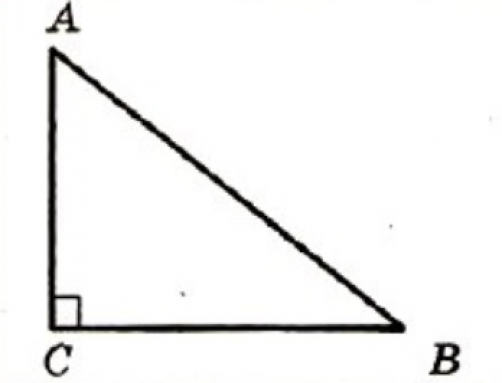
На рисунке в прямоугольном треугольнике АВ2=АС2+ВС2
Например, если в данном треугольнике катеты равны 9 и 12 см, то можно найти длину гипотенузы, используя теорему: АВ2=92+122=81+144=225=152, значит АВ=15 см.
Определение
Треугольник со сторонами 3, 4 и 5 см называют Египетским треугольником.
Пифагоровы тройки
Определение
Тройки чисел, которые удовлетворяют теореме Пифагора, называют Пифагоровы тройки, а сами числа – Пифагоровы числа. Например, такими являются числа 16, 12 и 20 – это числа, которые при подстановке в формулу теоремы, дают нам верное равенство: 162+122=202, 256+144=400, 400=400.
Способ под номером 3: даны катет и угол, который лежит напротив него
Чтобы не запутаться в формулах, введем обозначение для этого угла — β, а сторону оставим прежнюю «а». В этом случае потребуется другая тригонометрическая функция — синус.
Как и в предыдущем примере, синус равен отношению катета к гипотенузе. Формула этого способа выглядит так:
с = а / sin β.
Для того чтобы не запутаться в тригонометрических функциях, можно запомнить простое мнемоническое привило: если в задаче идет речь о противолежащем угле, то нужно использовать синус, если — о прилежащем, то косинус
Следует обратить внимание на первые гласные в ключевых словах. Они образуют пары о-и или и-о
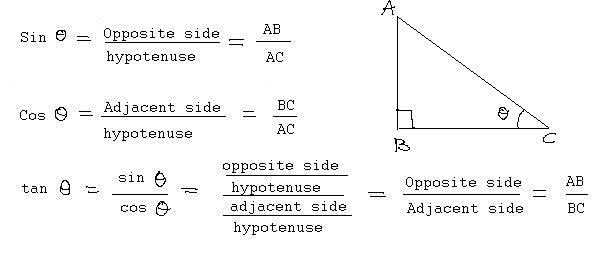
30-60-90 Доказательство теоремы о треугольнике
Дан треугольник ABC с прямым углом C, угол A = 30 °, угол B = 60 °, BC = a, AC = b и AB = c. Нам нужно доказать, что c = 2a и b = квадратный корень из a.
30-60-90 Подробное доказательство теоремы о треугольнике
Заявления
Причины
1. Прямой треугольник ABC с углом A = 30 °, углом B = 60 ° и углом C = 90 °.
1. Учитывая
2. Пусть Q — середина стороны AB.
2. Каждый сегмент имеет ровно одну среднюю точку.
3. Постройте сторону CQ, медиану стороны гипотенузы AB.
3. Постулат прямой / определение медианы треугольника.
4. CQ = ½ AB
4. Теорема о медиане.
5. AB = BQ + AQ
5. Определение промежуточности
6. BQ = AQ
6. Определение медианы треугольника.
7. AB = AQ + AQ
7. Закон замещения
8. AB = 2AQ
8. Дополнение
9. CQ = ½ (2AQ)
9. Закон замещения
10. CQ = AQ
10. Мультипликативный обратный
11. CQ = BQ
11. TPE
12. CQ = AQ; CQ = BQ
12. Определение конгруэнтных сегментов.
13. B = ∠ BCQ.
13. Теорема о равнобедренном треугольнике.
14. m∠ B = m∠ BCQ
14. Определение конгруэнтных сторон
15. m∠ BCQ = 60
15. TPE
16. m∠ B + m∠ BCQ + m∠BQC = 180
16. Сумма углов треугольника равна 180.
17. 60 + 60 + m∠ BQC = 180
17. Закон замещения
18. m∠ BQC = 60
18. APE
19. Треугольник BCQ равносторонний и, следовательно, равносторонний.
19. Определение равностороннего треугольника.
20. BC = CQ
20. Определение равностороннего треугольника.
21. BC = ½ AB
21. TPE
Чтобы доказать, что AC = √3BC, мы просто применим теорему Пифагора, c 2 = a 2 + b 2 .
AB 2 = (1 / 2AB) 2 + AC 2
AB 2 = (AB 2 ) / 4 + AC 2
(3/4) (AB 2 ) = AC 2
(√3 / 2) AB = AC
√3BC = AC
Ранее доказанная теорема говорит нам, что если нам дан треугольник 30-60-90, как на рисунке с 2x в качестве гипотенузы, длины катетов будут отмечены.
30-60-90 Формула треугольника и таблица горячих клавиш
Джон Рэй Куэвас
Способ под номером 4: по радиусу описанной окружности
Теперь, для того чтобы узнать, как найти гипотенузу, потребуется вспомнить свойство окружности, которая описана около прямоугольного треугольника. Оно гласит следующее. Центр окружности совпадает с серединой гипотенузы. Если сказать по-другому, то самая большая сторона прямоугольного треугольника равна диагонали окружности. То есть удвоенному радиусу. Формула для этой задачи будет выглядеть так:
с = 2 * r, где буквой r обозначен известный радиус.
Это все возможные способы того, как находить гипотенузу прямоугольного треугольника. Пользоваться в каждой конкретной задаче нужно тем методом, который больше подходит по набору данных.
Периметр треугольника, онлайн расчет
Как найти периметр треугольника по длине его сторон, формула периметра треугольника.
Периметр треугольника, онлайн расчет
|
c – гипотенуза a,b – катеты, образующие прямой угол Некоторые свойства прямоугольных треугольниковСвойство 1. Сумма двух острых углов прямоугольного треугольника равна 90°. Действительно. Поскольку сумма углов треугольника равна 180°, а прямой угол равен 90°, то сумма остальных углов равен 90°. Свойство 2. Если катет прямоугольного треугольника лежит напротив угла в 30°, то он равен половине гипотенузы. Доказательство. Рассмотрим прямоугольный треугольник ACB, у которого угол C прямой, а угол ∠ABC=30°. Приложим к этому треугольнику равному ему прямоугольный треугольник как показано на Рис.2. Рассмотрим треугольник ADB. Так как ∠A=∠D=∠ABD=60°, то треугольник ABD равносторонний. Следовательно AB=AD=BD. Тогда . Конец доказательства. Свойство 3. Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против данного катета равен 30°. Доказательство. Пусть у прямоугольного треугольника катет AC равен половине гипотенузы AB. Аналогично вышеизложенному приложим к этому треугольнику равному ему прямоугольный треугольник BCD(Рис.2). Получим равносторонний треугольник, где AB=AD=BD. Тогда ∠A=∠D=∠ABD=60°. Но ∠ABD=2∠ABС. Следовательно . Конец доказательства. |
|
| Помощь в решении задач по геометрии, учебник онлайн (все калькуляторы по геометрии). | |
| Калькуляторы по геометрии |
Примеры решения задачПРИМЕР 1
ПРИМЕР 2
Стороны прямоугольного треугольника Признаки прямоугольного треугольника Признаки равенства треугольников Высота в прямоугольном треугольнике Остроугольный треугольник |
|||||||||||||
| Треугольник. Виды, свойства, решение треугольников. | |||||||||||||
| Свойства треугольника. |
Способ под номером 4: по радиусу описанной окружности
Теперь, для того чтобы узнать, как найти гипотенузу, потребуется вспомнить свойство окружности, которая описана около прямоугольного треугольника. Оно гласит следующее. Центр окружности совпадает с серединой гипотенузы. Если сказать по-другому, то самая большая сторона прямоугольного треугольника равна диагонали окружности. То есть удвоенному радиусу. Формула для этой задачи будет выглядеть так:
с = 2 * r, где буквой r обозначен известный радиус.
Это все возможные способы того, как находить гипотенузу прямоугольного треугольника. Пользоваться в каждой конкретной задаче нужно тем методом, который больше подходит по набору данных.
Формулы и свойства прямоугольного треугольника
Обозначения формул:
(см. рисунок выше)
a, b — катеты прямоугольного треугольника
c — гипотенуза
α, β — острые углы треугольника
S — площадь
h — высота, опущенная из вершины прямого угла на гипотенузу
ma— медиана, проведенная к стороне a из противолежащего угла (α)
mb — медиана, проведенная к стороне b из противолежащего угла (β)
mc — медиана, проведенная к стороне c из противолежащего угла (γ)
В прямоугольном треугольнике любой из катетов меньше гипотенузы (Формулы 1 и 2). Данное свойство является следствием теоремы Пифагора.
Косинус любого из острых углов меньше единицы (Формулы 3 и 4). Данное свойство следует из предыдущего. Так как любой из катетов меньше гипотенузы, то из соотношение катета к гипотенузе всегда меньше единицы.
Квадрат гипотенузы равен сумме квадратов катетов (теорема Пифагора). (Формула 5). Это свойство постоянно используется при решении задач.
Площадь прямоугольного треугольника равна половине произведения катетов (Формула 6)
Сумма квадратов медиан к катетам, равна пяти квадратам медианы к гипотенузе и пяти квадратам гипотенузы, деленных на четыре (Формула 7). Кроме указанной, есть еще 5 формул, поэтому рекомендуется ознакомиться также и с уроком «Медиана прямоугольного треугольника», в котором более подробно изложены свойства медианы.
Высота прямоугольного треугольника равна произведению катетов, деленному на гипотенузу (Формула 8)
Квадраты катетов обратно пропорциональны квадрату высоты, опущенной на гипотенузу (Формула 9). Данное тождество также является одним из следствий теоремы Пифагора.
Длина гипотенузы равна диаметру (двум радиусам) описанной окружности (Формула 10). Гипотенуза прямоугольного треугольника является диаметром описанной окружности. Это свойство часто используется при решении задач.
Радиус вписанной в прямоугольный треугольник окружности можно найти как половину от выражения, включающего в себя сумму катетов этого треугольника минус длину гипотенузы. Или как произведение катетов, деленное на сумму всех сторон (периметр) данного треугольника. (Формула 11) Синус угла А (α, альфа) в прямоугольном треугольнике будет равен отношению противолежащего данному углу катета к гипотенузе (по определению синуса). (Формула 12). Данное свойство используется при решении задач. Зная величины сторон, можно найти угол, который они образуют.
Косинус угла А (α, альфа) в прямоугольном треугольнике будет равен отношению прилежащего данному углу катета к гипотенузе (по определению синуса). (Формула 13)
См. также Соотношения между углами и сторонами прямоугольного треугольника изучает Тригонометрия.
Содержание главы:
Прямоугольный треугольник
Биссектриса в прямоугольном треугольнике
Высота в прямоугольном треугольнике
Высота в прямоугольном треугольнике (Часть 2)
Теорема Пифагора и ее доказательство
Применение теоремы Пифагора
Гипотенуза прямоугольного треугольника
Перпендикуляр к плоскости прямоугольного треугольника
Подобие треугольников. Использование в задачахОписание курса Прямоугольный треугольник
Как найти гипотенузу: 4 способа поиска ответа
После изучения темы про прямоугольные треугольники ученики часто выбрасывают из головы всю информацию о них. В том числе и то, как найти гипотенузу, не говоря уже о том, что это такое.

И напрасно. Потому что в дальнейшем диагональ прямоугольника оказывается этой самой гипотенузой, и ее нужно найти. Или диаметр окружности совпадает с самой большой стороной треугольника, один из углов которого прямой. И найти ее без этого знания невозможно.
Существует несколько вариантов того, как найти гипотенузу треугольника. Выбор метода зависит от исходного набора данных в условии задачи величин.
Пример задачи №1
Условие: в прямоугольном треугольнике проведены медианы к обоим катетам. Длина той, которая проведена к большей стороне, равна √52. Другая медиана имеет длину √73. Требуется вычислить гипотенузу.
Так как в треугольнике проведены медианы, то они делят катеты на два равных отрезка. Для удобства рассуждений и поиска того, как найти гипотенузу, нужно ввести несколько обозначений. Пусть обе половинки большего катета будут обозначены буквой «х», а другого — «у».
Теперь нужно рассмотреть два прямоугольных треугольника, гипотенузами у которых являются известные медианы. Для них нужно дважды записать формулу теоремы Пифагора:
(2у) 2 + х 2 = (√52) 2
(у) 2 + (2х) 2 = (√73) 2 .
Эти два уравнения образуют систему с двумя неизвестными. Решив их, легко можно будет найти катеты исходного треугольника и по ним его гипотенузу.
Сначала нужно все возвести во вторую степень. Получается:
Из второго уравнения видно, что у 2 = 73 — 4х 2 . Это выражение нужно подставить в первое и вычислить «х»:
4(73 — 4х 2 ) + х 2 = 52.
292 — 16 х 2 + х 2 = 52 или 15х 2 = 240.
Из последнего выражения х = √16 = 4.
Теперь можно вычислить «у»:
у 2 = 73 — 4(4) 2 = 73 — 64 = 9.
По данным условия получается, что катеты исходного треугольника равны 6 и 8. Значит, можно воспользоваться формулой из первого способа и найти гипотенузу:
√(6 2 + 8 2 ) = √(36 + 64) = √100 = 10.
Ответ: гипотенуза равна 10.


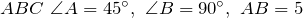 см. Найти .
см. Найти .





