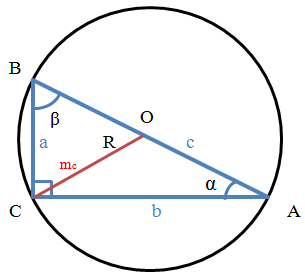
Формулы и свойства прямоугольного треугольника
Обозначения формул:
(см. рисунок выше)
a, b — катеты прямоугольного треугольника
c — гипотенуза
α, β — острые углы треугольника
S — площадь
h — высота, опущенная из вершины прямого угла на гипотенузу
ma— медиана, проведенная к стороне a из противолежащего угла (α)
mb — медиана, проведенная к стороне b из противолежащего угла (β)
mc — медиана, проведенная к стороне c из противолежащего угла (γ)
В прямоугольном треугольнике любой из катетов меньше гипотенузы (Формулы 1 и 2). Данное свойство является следствием теоремы Пифагора.
Косинус любого из острых углов меньше единицы (Формулы 3 и 4). Данное свойство следует из предыдущего. Так как любой из катетов меньше гипотенузы, то из соотношение катета к гипотенузе всегда меньше единицы.
Квадрат гипотенузы равен сумме квадратов катетов (теорема Пифагора). (Формула 5). Это свойство постоянно используется при решении задач.
Площадь прямоугольного треугольника равна половине произведения катетов (Формула 6)
Сумма квадратов медиан к катетам, равна пяти квадратам медианы к гипотенузе и пяти квадратам гипотенузы, деленных на четыре (Формула 7). Кроме указанной, есть еще 5 формул, поэтому рекомендуется ознакомиться также и с уроком «Медиана прямоугольного треугольника», в котором более подробно изложены свойства медианы.
Высота прямоугольного треугольника равна произведению катетов, деленному на гипотенузу (Формула 8)
Квадраты катетов обратно пропорциональны квадрату высоты, опущенной на гипотенузу (Формула 9). Данное тождество также является одним из следствий теоремы Пифагора.
Длина гипотенузы равна диаметру (двум радиусам) описанной окружности (Формула 10). Гипотенуза прямоугольного треугольника является диаметром описанной окружности. Это свойство часто используется при решении задач.
Радиус вписанной в прямоугольный треугольник окружности можно найти как половину от выражения, включающего в себя сумму катетов этого треугольника минус длину гипотенузы. Или как произведение катетов, деленное на сумму всех сторон (периметр) данного треугольника. (Формула 11) Синус угла А (α, альфа) в прямоугольном треугольнике будет равен отношению противолежащего данному углу катета к гипотенузе (по определению синуса). (Формула 12). Данное свойство используется при решении задач. Зная величины сторон, можно найти угол, который они образуют.
Косинус угла А (α, альфа) в прямоугольном треугольнике будет равен отношению прилежащего данному углу катета к гипотенузе (по определению синуса). (Формула 13)
См. также Соотношения между углами и сторонами прямоугольного треугольника изучает Тригонометрия.
Содержание главы:
Прямоугольный треугольник
Биссектриса в прямоугольном треугольнике
Высота в прямоугольном треугольнике
Высота в прямоугольном треугольнике (Часть 2)
Теорема Пифагора и ее доказательство
Применение теоремы Пифагора
Гипотенуза прямоугольного треугольника
Перпендикуляр к плоскости прямоугольного треугольника
Подобие треугольников. Использование в задачахОписание курса Прямоугольный треугольник
Что представляют собой сварочные стыки, их разновидности
Особенности устройства сварочных креплений оказывают влияние на физико-механическое характеристики конструкции и расход материала электрода. При выполнении выпуклых швов практически во всех случаях необходима их дополнительная обработка в виде снятия неровности, которая производится механическим методом. Исходя из формы поверхности, различают сварочные швы и их дефекты.
Действующими стандартными определяется несколько видов стыков, для распознавания которых используются буквенные обозначения швов сварных соединений.
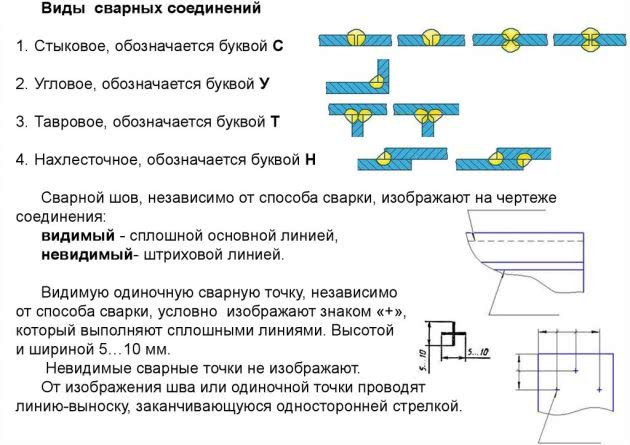 Обозначние сварных соединений
Обозначние сварных соединений
Стыковой вид
Для маркировки швов применяется буква «С». С помощью такого метода производится сварка деталей, расположенных в одной плоскости, стыкованием смежных торцов. Эти типы относятся к наиболее прочным и долговечным, они нашли широкое применение при изготовлении конструкций из металла, относящихся к категории ответственных. Для выполнения крепления необходимо провести тщательную подготовку поверхности.
 Виды стыковых соединений
Виды стыковых соединений
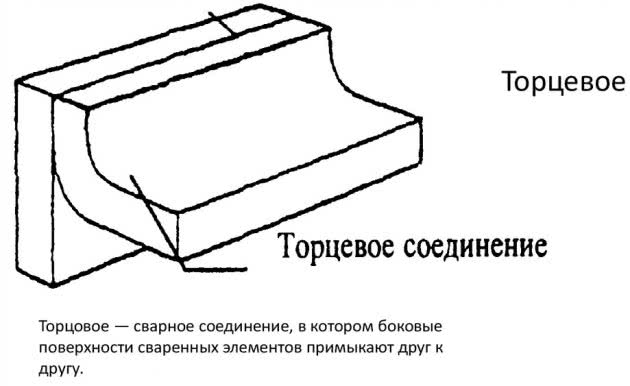
Торцевое крепление
И они обозначаются буквой «С». Формирование этих соединений производится по торцам заготовок. Торцевой стык часто применяется для сварки изделий из тонкого металла. При помощи такого крепления обеспечивается надежная фиксация деталей.
Нахлесточный вид
Стыки маркируются литерой «Н». При проведении сварочных работ с использованием таких приемов к качеству работы предъявляются менее строгие требования. Но прочностные характеристики и нагрузочная способность стыков гораздо хуже, чем у двух предыдущих вариантов. Для проведения крепления детали располагаются параллельно, со смещением относительно друг друга и частичным перекрытием.
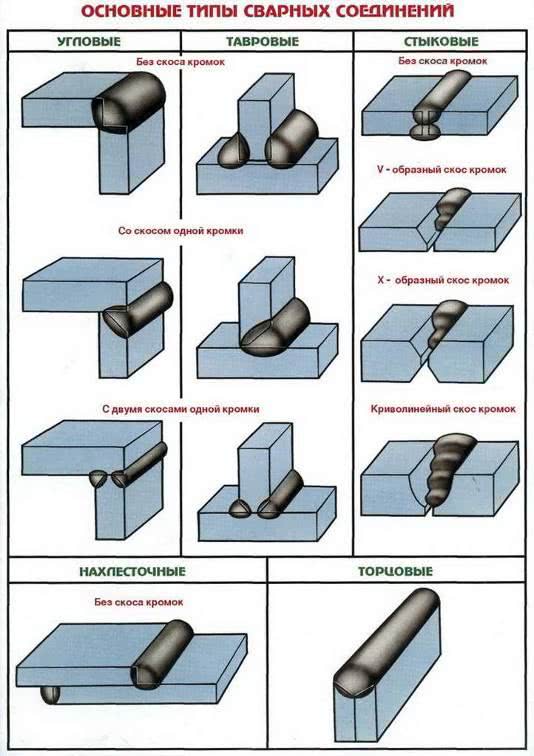
Тавровое крепление
Для обозначения швов сварных соединений используется буква «Т». Стыковка при помощи таврового метода относится к категории наиболее долговечных и жестких, но она плохо переносит нагрузку на изгиб. Для проведения работ одна из деталей располагается в горизонтальной плоскости, а вторая – вертикально, и сваривается торцом.
 Типы тавровых соединений
Типы тавровых соединений
Угловой вид
Стыки обозначаются литерой «У». Эти виды применяются реже остальных. Они надежны и долговечны. В зависимости от необходимости, детали располагаются относительно друг друга под разными углами.
Сварочные соединения всех типов могут выполняться односторонними, когда сварка производится только с одной стороны заготовки (обозначающимися «SS»), и двусторонними, маркирующимися «BS». В последнем случае детали свариваются с двух сторон.
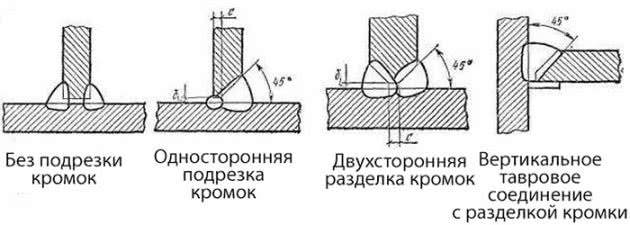
Обработка кромок
При проведении сварочных работ необходимо выполнить раздел кромок. Правильная их подгонка позволяет добиться:
- минимального расхода материалов;
- оптимального времени для сварки, выполняемой за один проход;
- прочности стыка, не уступающего по своим характеристикам основному металлу.
Применяется множество вариантов, различающихся углами, величиной зазора и т. д. Форма разделки выбирается в зависимости от способа сварки и толщины металлической заготовки. Чтобы качественно провести крепление, следует между кромками оставить зазор размером 4 мм.
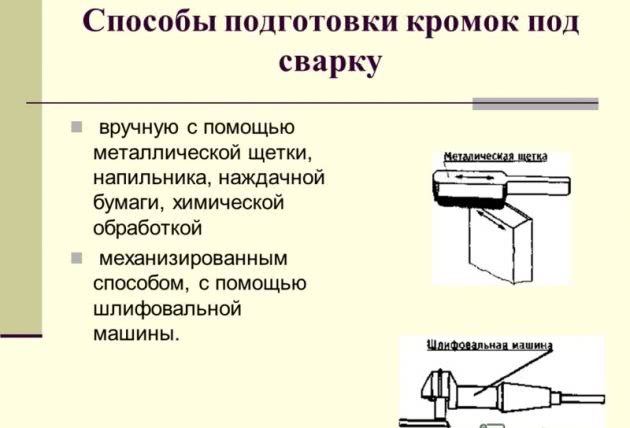
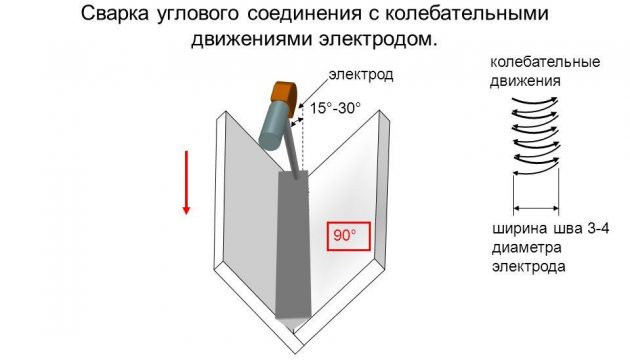
Разделка кромок может быть выполнена:
Под прямым углом.
Такой вариант используется при проведении односторонней сварки металла толщиной не более 3 мм, двустороннего крепления металла, имеющего толщину не более 8 мм, и для стыковки стали толщиной 4…8 мм.
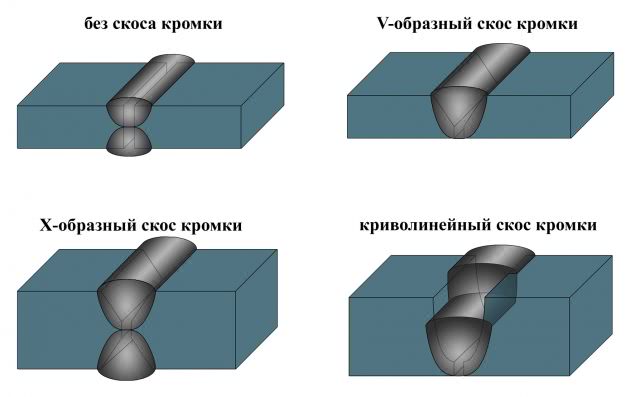
- В V-образной форме (односторонний скос). Толщина металла может быть 4…26 мм.
- В X-образной форме (двусторонний скос). Эта разделка применяется при креплении деталей толщиной 12…40 мм.
- Под углом 45 градусов. Такой вариант используется для металлов толщиной от 2 см.
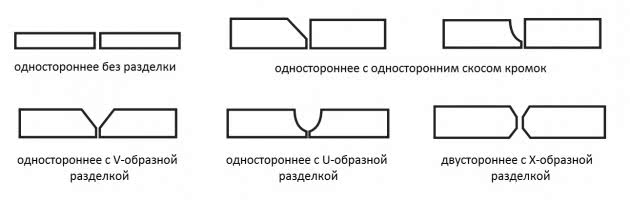 Виды кромок
Виды кромок
Задача про медиану в прямоугольном треугольнике
Медианы прямоугольного треугольника, проведенные к катетам, равны, соответственно, 3 см и 4 см. Найдите гипотенузу треугольника
Решение
Прежде чем начать решение задачи, обратим внимание на соотношение длины гипотенузы прямоугольного треугольника и медианы, которая опущена на нее. Для этого обратимся к формулам 2, 4, 5 свойств медианы в прямоугольном треугольнике
В этих формулах явно указано соотношение гипотенузы и медианы, которая на нее опущена как 1 к 2. Поэтому,для удобства будущих вычислений (что никак не повлияет на правильность решения, но сделает его более удобным), обозначим длины катетов AC и BC через переменные x и y как 2x и 2y (а не x и y).
Рассмотрим прямоугольный треугольник ADC. Угол C у него прямой по условию задачи, катет AC — общий с треугольником ABC, а катет CD равен половине BC согласно свойствам медианы. Тогда, по теореме Пифагора
AC2 + CD2 = AD2
Поскольку AC = 2x, CD = y (так как медиана делит катет на две равные части), то
4×2 + y2 = 9
Одновременно, рассмотрим прямоугольный треугольник EBC. У него также угол С прямой по условию задачи, катет BC является общим с катетом BC исходного треугольника ABC, а катет EC по свойству медианы равен половине катета AC исходного треугольника ABC.
По теореме Пифагора:
EC2 + BC2 = BE2
Поскольку EC = x (медиана делит катет пополам), BC = 2y, то
x2 + 4y2 = 16
Так как треугольники ABC, EBC и ADC связаны между собой общими сторонами, то оба полученных уравнения также связаны между собой.
Решим полученную систему уравнений.
4×2 + y2 = 9
x2 + 4y2 = 16
Сложим оба уравнения (впрочем, можно было выбрать и любой другой способ решения).
5×2 + 5y2 = 25
5( x2 + y2 ) = 25
x2 + y2 = 5
Обратимся к исходному треугольнику ABC. По теореме Пифагора
AC2 + BC2 = AB2
Так как длина каждого из катетов нам «известна», мы приняли, что их длина равна 2x и 2y, то есть
4×2 + 4y2 = AB2 Так как оба слагаемых имеют общий множитель 4, вынесем его за скобки
4 ( x2 + y2 ) = AB2
Чему равно x2 + y2 мы уже знаем (см. выше x2 + y2 = 5), поэтому просто подставим значения вместо x2 + y2
AB2 = 4 х 5
AB2 = 20
AB = √20 = 2√5
Ответ: длина гипотенузы равна 2√5
Угол между высотой и медианой треугольникаОписание курса Медіана прямокутного трикутника
Понятия и определения
Знак треугольника в первом веке ввёл в обиход древнегреческий философ и учёный Герон. Его свойства изучали Платон и Евклид. По их мнению, вся поверхность прямолинейного вида состоит из множеств различных треугольников. В геометрии под ними понимается область, лежащая в плоскости, ограниченной тремя отрезками, соединяющимися в трёх точках, не принадлежащих одной прямой.
Линии, образующие область, называются сторонами, а точки соприкосновения отрезков — вершинами. Основными элементами многоугольника являются:
- Медиана — отрезок, соединяющий середину с противолежащим углом. В треугольнике три медианы, которые пересекаются в одной точке. Называется она центроидом и определяет центр тяжести объекта.
- Высота — линия, опущенная из вершины на противоположную сторону, образующую с ней прямой угол. Место пересечения высот называют ортоцентром.
- Биссектриса — прямая, проведённая из угла таким образом, что делит его на две равные части. Если в треугольник вписать окружность, соприкасающуюся с его сторонами, то её центр совпадёт с точкой пересечения биссектрис. Называют это место — инцентр.
Различают треугольники и по числу равных сторон. Так, если они все равны, фигура называется равносторонней. Когда же по величине совпадают только две стороны, то многоугольник является равнобедренным. Его главное свойство в том, что углы равны. Частным случаем равнобедренного многоугольника является правильный треугольник (разносторонний).
Чтобы не возникала путаница, существуют стандартные обозначения величин. Вершины подписываются заглавными буквами A, B, C, а углы — греческими символами: α, β, γ. Стороны же обозначают прописными буквами латинского алфавита: a, b, c.
Типы сварочных соединений и условные обозначения
Для качественного соединения отдельных элементов при создании металлоконструкций необходимо иметь подробное описание каждого стыка. Для этого выполняется состоящая из чертежей конструкторская документация, в которой все условные обозначения сварных швов должны соответствовать ГОСТам.
В зависимости от способов стыковки свариваемых друг с другом элементов различают несколько видов соединений. Наименования, особенности и обозначение сварочных швов на чертежах можно посмотреть в таблице ниже.
| Типы швов | Характеристики | Сварочный шов на чертеже |
| Стыковой | Расположенные в одной плоскости детали свариваются по прилегающим торцам. Чтобы стыки получались ровными и прочными необходимо перед соединением обработать стыковые кромки | С |
| Угловой | Детали соединяются по наклоненным один к другому торцам, угол между которыми должен составлять более 30° | У |
| Торцевой | Соединяются торцы элементов таким образом, чтобы между собой соприкасались боковые поверхности | С |
| Нахлесточный | Одна на другую накладываются плоскости элементов. Используются в случаях, когда точность подгонки не является критичной | Н |
| Тавровый | К поверхности конструкции под углом или вертикально приваривается торец детали | Т |
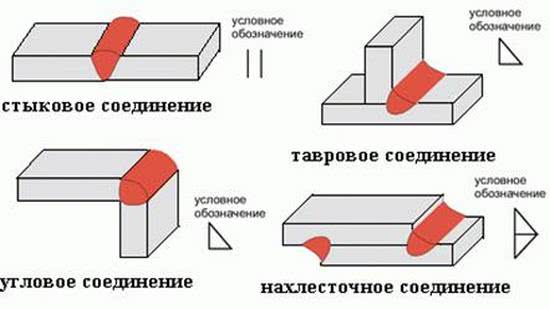
Существуют также не предусмотренные ГОСТом особые виды швов, которые на схемах обозначаются символом «О».
По расположению
- Односторонние (SS) если предстоит сваривание деталей только с одной стороны
- Двусторонние (BS) для того, чтобы сделать именно такой тип соединения, необходимо перемещать сварочный аппарат поочередно с верхней части рабочей поверхности к внутренней. При этом внутри сечения будет находиться корень стыкового шва.
По способу выполнения (протяженности сварки)
- точечными;
- сплошными;
- прерывистыми (предусматривается определенный и постоянный интервал между касанием сварки
Обозначение прерывистого (не сплошного) сварного шва на чертеже — это сплошная линия (если это видимые стыки) а если они не видимы, то линия будет штриховая.
Данный вид шва в свою очередь делится на три подвида: точечный, цепной и шахматный
По форме разделки кромок
- Без разделкиДля того чтобы сварка методом плавления производилась на оптимальной глубине и максимально качественно, для этого необходимо разделить кромки. Это возможно сделать несколькими способами:
- Односторонняя разделка
- 2х сторонняя разделка
Свойства прямоугольного треугольника:
1. В прямоугольном треугольнике сумма двух острых углов равна 90°.
2. В прямоугольном треугольнике катет, лежащий против угла в 30° , равен половине гипотенузы.
И наоборот, если в прямоугольном треугольнике катет вдвое меньше гипотенузы, то напротив него лежит угол в 30˚.
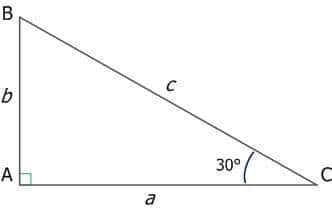
Рис. 7. Прямоугольный треугольник с острым углом 30˚
b = c / 2
3. Теорема Пифагора:
Сумма квадратов катетов равна квадрату гипотенузы.
c2 = a2 + b2 ,
где a, b – катеты, c – гипотенуза.
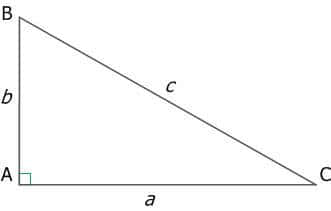
Рис. 8. Прямоугольный треугольник
4. В прямоугольном треугольнике центр описанной окружности – есть середина гипотенузы.
И соответственно радиус описанной окружности (R) равен половине гипотенузы.
,
где c – гипотенуза.
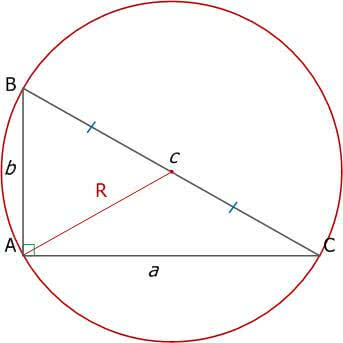
Рис. 9. Прямоугольный треугольник и описанная окружность
5. В прямоугольном треугольнике медиана, падающая на гипотенузу, равна половине гипотенузы.
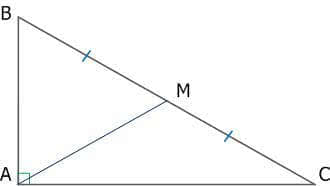
Рис. 10. Прямоугольный треугольник и медиана, падающая на гипотенузу
АМ – медиана прямоугольного треугольника, падающая на гипотенузу, АМ = ВМ = МС, АМ = ВС/2
6. В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника подобные исходному.
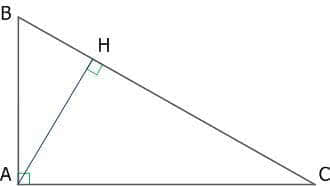
Рис. 11. Прямоугольный треугольник и высота, проведенная из вершины прямого угла
АВ/ВС = АН/АС = ВН/АВ
Геометрия сварного шва
Рассмотрев разновидности мест, где катет может иметь свои параметры и особенности, стоит взглянуть на другие составляющие сварного соединения, которые также могут оказаться важными. Многие величины взаимозависимы, но некоторые можно доработать уже после создания шва. К примеру, высота валика всегда может стать меньше при обтачивании, если это необходимо. Основные параметры выглядят следующим образом:
Схема обтачивания сварного шва
- E – ширина полученного шва;
- T – толщина созданного шва;
- B – зазор между свариваемыми деталями;
- H – глубина залегания области проварки;
- S – толщина используемой заготовки;
- Q – размер выпуклой части.
Для углового соединения они несколько отличаются, так как здесь другое геометрическое положение
Тем не менее, важность из значения не становится меньше. Здесь выделяют:
Схема углового соединения
- K – катет шва;
- A – Величина толщины углового шва, к которой относится величина расчетной высоты и выпуклости;
- Q – выпуклость наплавленной области;
- P – расчетная высота, что должна соответствовать перпендикулярной линии, которая проводится из места наиболее глубокого проплавления к гипотенузе наибольшего прямого треугольника, который вписан во внешнюю часть шва.
Свойства
Разобравшись с тем, что такое катет сварного шва, следует отметить свойства, которыми должно обладать соединение. В первую очередь это однородность и равномерность наплавленного валика. Это легко определиться, так как здесь может применяться даже визуально-измерительный контроль сварных швов, самый простой и доступный из них. Высота валика должна быть примерно одинаковой по всей поверхности. Это же касается и его ширины, так как в этом случае нагрузки на нем будут распространяться равномерно. Если будет какое-либо послабление, то вероятность поломки возрастает именно в этом месте.
Однородность состава обеспечивает лучшее скрепление. Как правило, различные марки металла очень плохо свариваются и чем больше различий в составе, тем хуже будут скреплены заготовки. Для высокого качества соединения следует знать, какие электроды выбрать для сварки инвертором, или другим удобным способом. Также следует рассчитать правильное геометрическое расположение шва, чтобы у него был максимальный охват скрепляемых деталей.
Не менее важным параметром является глубина проварки. Если заготовки будут соединены не по всей возможной площади, то они не смогут выдерживать максимальные нагрузки. В профессиональной сфере рассчитывается каждый параметр соединения, чтобы придать конструкции максимальную прочность. Здесь нужно знать, как рассчитать катет сварного шва, чтобы он приобрел требуемые параметры и как провести сварку.
Выбор катета шва
Расчет катета сварного шва совершается под каждое отдельное соединение. Чтобы правильно выбрать его, требуется знать параметры свариваемых деталей. Прочность здесь будет зависеть от толщины соединения и его длины. Основным параметром выбора и расчета является длина, так как от этого зависит прочность. Слишком большая длина приведет к увеличению расхода материалов, а также деформации заготовки.
Схема чтения длины катета сварного шва
На практике применяются разнообразные шаблоны, которые проверены опытом предыдущих сварщиков. Для каждого типа соединения, в зависимости от размера заготовки и положения, подбирают готовые размеры.
Как измерить катет сварного шва
Разобравшись с тем, как выбрать катет сварного шва, необходимо узнать, как правильно провести его измерения. Это требуется для того, чтобы проконтролировать полученный результат. Размер искомого значения определяется по обыкновенным геометрическим законам. Для этого требуется вычислить катет максимально возможного треугольника, вписанного в продольное сечение соединения. Итоговый размер катета соединения и будет искомой величиной.
Схема определения катета сварного шва
Как рассчитать катет сварного шва
В каждом случае, расчет проводится по-разному, в зависимости от имеющихся условий. К примеру, для определения нахлесточных соединений листов, толщина которых составляет менее 4 мм, катет стараются делать равным по толщине самих листов. Если же толщина листов составляет больше 4 мм, то здесь берется 40% от толщины металла и добавляется 2 мм. Таким и должен быть максимальный катет сварного шва.
Онлайн калькулятор
Чтобы вычислить длины сторон прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):
- для гипотенузы (с):
- длины катетов a и b
- длину катета (a или b) и прилежащий к нему острый угол (β или α, соответственно)
- длину катета (a или b) и противолежащий к нему острый угол (α или β, соответственно)
- для катета:
- длину гипотенузы (с) и длину одного из катетов
- длину гипотенузы (с) и прилежащий к искомому катету (a или b) острый угол (β или α, соответственно)
- длину гипотенузы (с) и противолежащий к искомому катету (a или b) острый угол (α или β, соответственно)
- длину одного из катетов (a или b) и прилежащий к нему острый угол (β или α, соответственно)
- длину одного из катетов (a или b) и противолежащий к нему острый угол (α или β, соответственно)
Введите их в соответствующие поля и получите результат.
Найти гипотенузу (c)
Найти гипотенузу по двум катетам
Катет a = Катет b = Гипотенуза c =
Чему равна гипотенуза (сторона с) если известны оба катета (стороны a и b)?
Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов:
c² = a² + b²
следовательно: c = √a² + b²
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 3 см, а катет b = 4 см:
c = √3² + 4² = √9 + 16 = √25 = 5 см
Найти гипотенузу по катету и прилежащему к нему острому углу
Катет (a или b) = Прилежащий угол (β или α) = Гипотенуза c =
Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и прилежащий к нему угол?
c = a/cos(β) = b/cos(α)
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а прилежащий к нему ∠β = 60°:
c = 2 / cos(60) = 2 / 0.5 = 4 см
Найти гипотенузу по катету и противолежащему к нему острому углу
Катет (a или b) = Противолежащий угол (α или β) = Гипотенуза c =
Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и противолежащий к нему угол?
c = a/sin(α) = b/sin(β)
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а противолежащий к нему ∠α = 30°:
c = 2 / sin(30) = 2 / 0.5 = 4 см
Найти гипотенузу прямоугольного треугольника только по двум острым углам невозможно.
Найти катет
Найти катет по гипотенузе и катету
Гипотенуза c = Катет (известный) = Катет (искомый) =
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и второй катет?
a = √c² — b²
b = √c² — a²
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 5 см, а катет b = 4 см:
a = √5² — 4² = √25 — 16 = √9 = 3 см
Найти катет по гипотенузе и прилежащему к нему острому углу
Гипотенуза c = Угол (прилежащий катету) = °Катет =
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и прилежащий к искомому катету острый угол?
a = c ⋅ cos(β)
b = c ⋅ cos(α)
Пример
Для примера посчитаем чему равен катет b прямоугольного треугольника если гипотенуза c = 5 см, а ∠α = 60°:
b = 5 ⋅ cos(60) = 5 ⋅ 0.5 = 2.5 см
Найти катет по гипотенузе и противолежащему к нему острому углу
Гипотенуза c = Угол (противолежащий катету) = °Катет =
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и противолежащий к искомому катету острый угол?
a = c ⋅ sin(α)
b = c ⋅ sin(β)
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 4 см, а ∠α = 30°:
a = 4 ⋅ sin(30) = 4 ⋅ 0.5 = 2 см
Найти катет по второму катету и прилежащему к нему острому углу
Катет (известный) = Угол (прилежащий известному катету) = °Катет (искомый) =
Чему равен один из катетов прямоугольного треугольника если известен другой катет и прилежащий к нему острый угол?
a = b ⋅ tg(α)
b = a ⋅ tg(β)
Пример
Для примера посчитаем чему равен катет b прямоугольного треугольника если катет a = 2 см, а ∠β = 45°:
b = 2 ⋅ tg(45) = 2 ⋅ 1 = 2 см
Найти катет по второму катету и противолежащему к нему острому углу
Катет (известный) = Угол (противолежащий известному катету) = °Катет (искомый) =
Чему равен один из катетов прямоугольного треугольника если известен другой катет и противолежащий к нему острый угол?
a = b / tg(β)
b = a / tg(α)
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если катет b = 3 см, а ∠β = 35°:
a = 3 / tg(35) ≈ 3 / 0.7 ≈ 4.28 см
Свойства геометрической фигуры
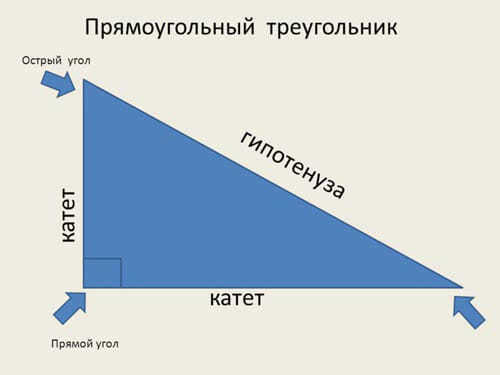
Перед тем, как найти гипотенузу треугольника, необходимо разобраться, какие особенности имеет данная фигура. Рассмотрим главные из них:
- В прямоугольном треугольнике оба острых угла в сумме будут равны 90º.
- Катет, лежащий против угла в 30º, будет равен ½ от величины гипотенузы.
- Если катет равен ½ от значения гипотенузы, тогда второй угол будет иметь такую же величину – 30º.
Найти гипотенузу в прямоугольном треугольнике можно несколькими способами. Самым простым решением является вычисление через катеты. Допустим, вам известны значения катетов сторон А и В. Тогда на выручку приходит теорема Пифагора, повествующая нам, что если поставить каждую величину катета в квадрат и просуммировать полученные данные, мы узнаем чему равна гипотенуза. Таким образом, нам необходимо просто извлечь значение квадратного корня:
Например, если катет А = 3 см, а катет В = 4 см, тогда вычисление будет иметь следующий вид:
Определение медианы
|
Медианой треугольника называется отрезок, соединяющий один из углов треугольника с серединой противолежащей ему стороны. (медианой также называют прямую, содержащую данный отрезок) |
- Медианы треугольника пересекаются в одной точке и делятся этой точкой на две части в отношении 2:1, считая от вершины угла. Точка их пересечения называется центром тяжести треугольника (относительно редко в задачах для обозначения этой точки используется термин «центроид»),
- Медиана разбивает треугольник на два равновеликих треугольника.
- Треугольник делится тремя медианами на шесть равновеликих треугольников.
- Большей стороне треугольника соответствует меньшая медиана.
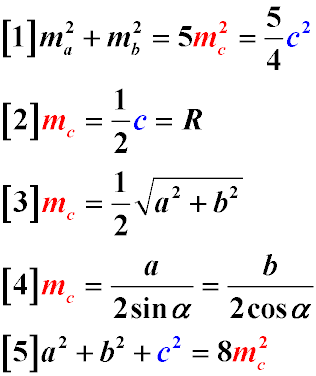
Задачи по геометрии, предлагаемые для решения, в основном, используют следующие свойства медианы прямоугольного треугольника.
- Сумма квадратов медиан, опущенных на катеты прямоугольного треугольника равна пяти квадратам медианы, опущенной на гипотенузу (Формула 1)
- Медиана, опущенная на гипотенузу прямоугольного треугольника равна половине гипотенузы (Формула 2)
- Медиана, опущенная на гипотенузу прямоугольного треугольника, равна радиусу окружности, описанной вокруг данного прямоугольного треугольника (Формула 2)
- Медиана, опущенная на гипотенузу, равна половине корня квадратного из суммы квадратов катетов (Формула 3)
- Медиана, опущенная на гипотенузу, равна частному от деления длины катета на два синуса противолежащего катету острого угла (Формула 4)
- Медиана, опущенная на гипотенузу, равна частному от деления длины катета на два косинуса прилежащего катету острого угла (Формула 4)
- Сумма квадратов сторон прямоугольного треугольника равна восьми квадратам медианы, опущенной на его гипотенузу (Формула 5)
Обозначения в формулах:
a, b — катеты прямоугольного треугольника
c — гипотенуза прямоугольного треугольника
Если обозначить треугольник, как ABC, то
ВС = а
AC = b
AB = c
(то есть стороны a,b,c — являются противолежащими соответствующим углам)
ma— медиана, проведенная к катету а
mb — медиана, проведенная к катету b
mc — медиана прямоугольного треугольника, проведенная к гипотенузе с
α (альфа) — угол CAB, противолежащий стороне а