Использование онлайн-конвертера
Десятичные дроби могут состоять из довольно больших чисел. Поэтому не всегда их можно быстро преобразовать. При этом любая невнимательность может привести к ошибке, что повлечёт неверный как промежуточный, так и итоговый результат. В таких случаях есть резон использовать так называемый конвертер дробей.
Это интернет-сервис, предоставляющий услуги по автоматическому преобразованию дробей из одного вида в другой. Для того чтобы воспользоваться его возможностями, пользователю даже необязательно понимать принцип перевода выражений. От него требуется лишь ввести исходные данные в предлагаемую форму и нажать кнопку «Рассчитать».
Таких математических сервисов в интернете довольно много. Русскоязычные конвертеры не требуют регистрации и указания каких-либо персональных данных. При этом свои услуги они предоставляют бесплатно. Согласно отзывам пользователей, можно выделить следующие онлайн-калькуляторы:

- 0oq,
- onlinemschool,
- naobumium,
- allcalc,
- webmath.
Нужно отметить, что приведенные сайты являются настоящими математическими комбайнами-решателями. Они умеют не только конвертировать дроби, но и выполнять с ними любые действия. Например, складывать, делить, умножать, извлекать корень и возводить в степень. Кроме этого, на их страницах содержится теоретический материал и подробное описание решений.
Примеры
Конечные дроби
Пример 1
0,2 =
2
Т.к. после запятой всего одна цифра, значит пишем один ноль после единицы в знаменателе, а в числитель переносим цифру 2.
Пример 2
0,02 =
2
Т.к. после запятой две цифры, значит пишем два нуля после единицы в знаменателе. А в числитель переносим только цифры, отличные от нуля.
Пример 3
0,02000 = 0,02 =
2
Т.к. нули после цифр в дробной части десятичной дроби можно отбросить, следовательно, остаются только две цифры, а значит – всего два нуля с единицей в знаменателе. Числитель, как и в примере выше, будет содержать только одну цифру 2.
Пример 4
3,8 = 3
8
Целую часть десятичной дроби переписываем в целую часть простой смешанной дроби, а дробную часть представляем в виде числителя и знаменателя. Полученную дробь, также, можно записать как неправильную.
3
8
=
3 ⋅ 10 + 8
=
38
Пример 5
6,27 = 6
27
(смешанная дробь)
6
27
=
6 ⋅ 100 + 27
=
627
(неправильная дробь)
Пример 6
8,09 = 8
9
(смешанная дробь)
8
9
=
8 ⋅ 100 + 9
=
809
(неправильная дробь)
Пример 7
10,607 = 10
607
=
10 ⋅ 1000 + 607
=
10607
Пример 8
15,040500 = 15,0405 = 15
405
=
15 ⋅ 10000 + 405
=
150405
Бесконечные дроби
Давайте переведем бесконечную дробь 12,004571231457668723568421… в обыкновенную.
Решение
Для начала округлим дробь до 4 цифр после запятой, т.е. 12,004571231457668723568421… ≈ 12,0046.
Теперь можем превратить эту дробь в простую.
12,0046 = 12
46
=
12 ⋅ 10000 + 46
=
120046
Что такое обыкновенная дробь?
Обыкновенной дробью зовется незавершенная операция деления или, проще говоря, какая-то часть целого. Долгое время, иначе как часть чего-то цельного дробь не воспринимали. Однако в развитии науки настал момент, когда потребовались точные вычисления. В это время и поняли, что дробью можно заменять деление, которое точно выполнить не получится.
После того, как деление заменяли дробью, последнюю использовали просто как число в дальнейших вычислениях, не теряя в точности. В зависимости от ситуации можно использовать любое определение дробей, оба являются верными.
В обыкновенной дроби числитель обозначает делимое, знаменатель делитель, а знак деления обозначает дробная черта. Ничего сложного в том, чтобы преобразовать дробь обратно в деление, нет. Приведем пример:
$>=5:6$ – чтобы проверить это утверждение можно взять калькулятор и использовать это число дважды в одной и той же операции. Так:
5:6*6=5 – в одном и том же примере на первой позиции мы сначала использовали дробь, а потом операцию деления. Результат не изменился и он не измениться в любых других подобных примерах.
Как перевести обычную дробь в десятичную
Прежде чем узнать, как от обычной записи перейти к десятичной, вспомним различия двух видов дробей и сформулируем важное правило. Десятичные дроби — это конструкции вида 0,5; 2,16 и -7,42
А так выглядят эти же числа в форме обыкновенных дробей:
Десятичные дроби — это конструкции вида 0,5; 2,16 и -7,42. А так выглядят эти же числа в форме обыкновенных дробей:
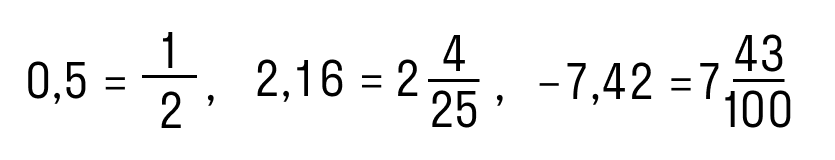
Обыкновенную дробь можно перевести в конечную десятичную дробь только при условии, что её знаменатель можно разложить на простые множители 2 и 5 любое количество раз. Например:
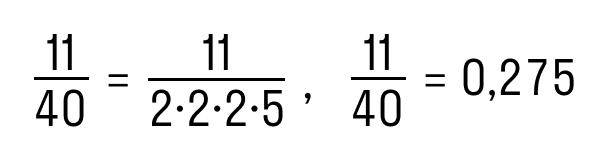
Дробь 11/40 можно преобразовать в конечную десятичную, потому что знаменатель раскладывается на множители 2 и 5.
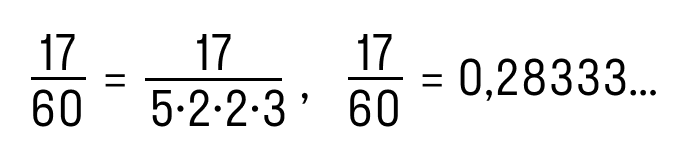
Дробь 17/60 нельзя преобразовать в конечную десятичную дробь, потому что в её знаменателе кроме множителей 2 и 5, есть 3.
А теперь перейдем к самому главному вопросу: рассмотрим несколько алгоритмов перевода обыкновенной дроби в десятичную.
Способ 2.
Я выберу три десятичные дроби: 3,86, 5,5 и 1,7, и сразу на их примере простыми словами расскажу, как из них получить обыкновенные.
Для начала мы смотрим, сколько знаков стоит после запятой.
3,86 – два знака; 5,5 – один знак; 1,007 – три знака.
Целую часть из дроби просто переписываем.
В числитель записываем дробную часть, а в знаменатель – 10 n , где n – количество знаков после запятой. То есть если один знак после запятой, то делим на 10 1 = 10, если два – на 10 2 = 100, если три – на 10 3 = 1000 и так далее.
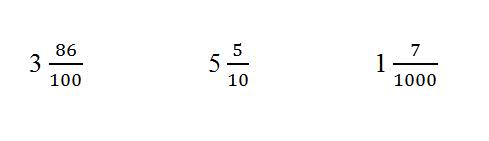
Теперь сокращаем дробь насколько это возможно – делим и числитель, и знаменатель на одно и то же число столько раз, пока у них не останется общих делителей.
Во втором способе уже есть подсказка, когда мы десятичную дробь произносим вслух. Например, дробь 3,86 мы произнесем как «три целых восемьдесят шесть сотых», 5,5 – «пять целых пять десятых», а 1,007 – «одна целая семь тысячных». Вот и подсказка: сотых – значит, делить надо на 100, десятых – на 10, тысячных – на 1000.
Второй способ гораздо быстрее первого, потому что мы сразу считаем количество знаков после запятой и делим на число 10, возведенное в такую же степень, как и количество знаков.
Сложение и вычитание дробей
При сложении и вычитании дробей с одинаковыми знаменателями к числителю первой дроби прибавляют числитель второй дроби (из числителя первой вычитают числитель второй) и оставляют тот же знаменатель.
Не забудьте проверить, можно ли сократить дробь и выделить целую часть.
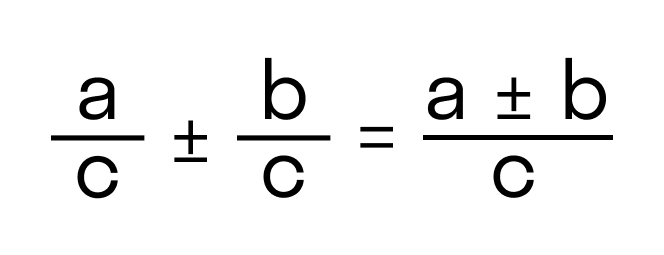
При сложении и вычитании дробей с разными знаменателями нужно найти наименьший общий знаменатель, сложить или вычесть полученные дроби (используем предыдущее правило).
Вот, что делать:
- Найдем наименьшее общее кратное для определения единого делителя.
Для этого запишем в столбик числа, которые в сумме дают значения делителей. Далее перемножаем полученное и получаем НОК.
НОК (15, 18) = 3 * 2 * 3 * 5 = 90
- Найдем дополнительные множители для каждой дроби. Для этого НОК делим на каждый знаменатель:
90 : 15 = 6,
90 : 18 = 5.
Полученные числа запишем справа сверху над числителем.
- Воспользуемся одним из основных свойств дробей: перемножим делимое и делитель на дополнительный множитель. После умножения делитель должен быть равен наименьшему общему кратному, которое мы ранее высчитывали. Затем можно перейти к сложению.
- Проверим полученный результат:
- если делимое больше делителя, нужно преобразовать в смешанное число;
- если есть что сократить, нужно выполнить сокращение.
Ход решения одной строкой:
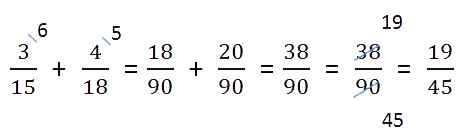
Сложение или вычитание смешанных чисел можно привести к отдельному сложению их целых частей и дробных частей. Для этого нужно действовать поэтапно:
- Сложить целые части.
- Сложить дробные части.
Необходимо приводить к общему, если знаменатели разные. Для этого воспользуемся знаниями из предыдущего примера.
- Суммировать полученные результаты.
Если при сложении дробных частей получилась неправильная дробь, нужно выделить ее целую часть и прибавить к полученной ранее целой части.
Преобразование десятичных дробей
Чтобы ни одна задача не смутила вас своей формулировкой, важно знать, как преобразовывать десятичные дроби в другие виды. Сейчас научимся!
Как перевести десятичную дробь в проценты
Уже в пятом классе задачки по математике намекают, что дроби как-то связаны с процентами. И это правда: процент — это одна сотая часть от любого числа, обозначают его значком %.
1% = 1/100 = 0,01
Чтобы узнать, как перевести проценты в дробь, нужно убрать знак % и разделить наше число на 100, как в примере выше.
А чтобы перевести десятичную дробь в проценты — умножаем дробь на 100 и добавляем знак %. Давайте на примере:
0,15 = 0,15 · 100% = 15%.
Выразить дробь в процентах просто: сначала превратим её в десятичную дробь, а потом применим предыдущее правило.
2/5 = 0,4
0,4 · 100% = 40%
8/25 = 0,32
0,32 · 100% = 32%
Чтобы разрезать торт на равные кусочки и не обижать гостей, нужно всего-то запомнить соотношения частей и целого. Наглядная табличка — наш друг-помощник:
Преобразование десятичных дробей
Быстрая напоминалка:
Десятичная дробь — это число с остатком, где остаток стоит после целой части и разделяется запятой.
Смешанная дробь — это тоже число с остатком, но остаток записывают в виде простой дроби (с черточкой).
Чтобы переводить десятичные дроби в смешанные, не нужно запоминать особые алгоритмы. Достаточно понимать определения и правильно читать заданную дробь — этим школьники и занимаются в 5 классе. А теперь давайте потренируемся!
Пример 1. Перевести 5,4 в смешанное число.
Как решаем:
- Читаем вслух: пять целых четыре десятых. «Четыре десятых» подсказывают, что в числителе будет 4, а в знаменателе — 10. В смешанном виде эта дробь выглядит так: 5 4/10.
- А теперь сократим числитель и знаменатель на два (потому что можно) и получим: 5 2/5.
Ответ: 5,4 = 5 2/5.
Пример 2. Перевести 4,005 в смешанное число.
Как решаем:
- Читаем вслух: четыре целых пять тысячных. Значит 5 — идет в числитель, а 1000 — в знаменатель. В смешанном виде получается так: 4 5/1000. После сокращения: 4 1/200.
Ответ: 4,005 = 4 1/200.
Пример 3. Перевести 5,60 в смешанное число.
Как решаем:
- Читаем вслух: пять целых шестьдесят сотых. Отправляем 60 в числитель, а 100 — в знаменатель. В смешанном виде дробь такая: 5 60/100.
- Сократим дробную часть на 10 и получим 5 6/10. Или можно вспомнить про свойство десятичной дроби и просто отбросить нули в числителе и знаменателе.
Ответ: 5,60 = 5 6/10.
Как перевести десятичную дробь в обыкновенную
Не будем придумывать велосипед и рассмотрим самый простой способ превращения десятичной дроби в обыкновенную. Вот, как это сделать:
- Перепишем исходную дробь в новый вид: в числитель поставим исходную десятичную дробь, а в знаменатель — единицу. Например:
- 0,35 = 0,35/1
- 2,34 = 2,34/1
- Умножим числитель и знаменатель на 10 столько раз, чтобы в числителе исчезла запятая. При этом после каждого умножения запятая в числителе сдвигается вправо на один знак, а у знаменателя соответственно добавляются нули. На примере легче:
- 0,35 = 0,35/1 = 3,5/10 = 35/100
- 2,34 = 2,34/1 = 23,4/10 = 234/100
- А теперь сокращаем — то есть делим числитель и знаменатель на кратные им числа:
- 0,35 = 35/100, делим числитель и знаменатель на пять, получаем 6/20, еще раз делим на 2, получаем итоговый ответ 3/10.
- 2,34 = 234/100 = 117/50 = 2 17/50.
Не забывайте про минус в ответе, если пример был про отрицательное число. Очень обидная ошибка!
Перевод обыкновенной дроби в десятичную
Не любую обыкновенную дробь можно перевести в десятичную, так как чтобы записать обыкновенную дробь в виде десятичной, надо привести её к знаменателю, представляющему собой единицу с одним или несколькими нулями, например: 10, 100, 1000 и т. д. Если разложить такой знаменатель на простые множители, то получится одинаковое количество двоек и пятёрок:
100 = 10 · 10 = 2 · 5 · 2 · 5;
1000 = 10 · 10 · 10 = 2 · 5 · 2 · 5 · 2 · 5.
Никаких других простых множителей эти разложения не содержат, следовательно:
Обыкновенную дробь можно представить в виде десятичной только в том случае, если её знаменатель не содержит никаких других множителей, кроме 2 и 5.
При разложении её знаменателя на простые множители получается произведение 2 · 2:
Перевод обыкновенных дробей в десятичные дроби
Обыкновенные дроби, у которых в знаменателе числа 10, 100, 1000 или 10000, тоже можно перевести в десятичные дроби. Поскольку у обыкновенной дроби целая часть отсутствует, сначала записывают 0, затем ставят запятую и записывают числитель дробной части.
Здесь также количество нулей в знаменателе и количество цифр в числителе должно быть одинаковым. Поэтому следует быть внимательным.
Пример 1. Перевести обыкновенную дробь в десятичную дробь.
Целая часть отсутствует, значит сначала записываем 0 и ставим запятую:
0,
Теперь смóтрим на количество нулей в знаменателе. Видим, что там один ноль. И в числителе одна цифра. Значит можно спокойно продолжить десятичную дробь, записав после запятой цифру 5
0,5
В полученной десятичной дроби 0,5 количество цифр после запятой и количество нулей в знаменателе дроби одинаково. Значит дробь переведена правильно.
Десятичная дробь 0,5 читается так:
«Ноль целых, пять десятых»
Пример 2. Перевести обыкновенную дробь в десятичную дробь.
Целая часть отсутствует. Записываем сначала 0 и стáвим запятую:
0,
Теперь смóтрим на количество нулей в знаменателе. Видим, что там два нуля. А в числителе только одна цифра. Чтобы сделать количество цифр и количество нулей одинаковым, добавим в числителе перед цифрой 2 один ноль. Тогда дробь примет вид . Теперь количество нулей в знаменателе и количество цифр в числителе одинаково. Значит можно продолжить десятичную дробь:
0,02
В полученной десятичной дроби 0,02 количество цифр после запятой и количество нулей в знаменателе дроби одинаково. Значит дробь переведена правильно.
Десятичная дробь 0,02 читается так:
«Ноль целых, две сотых».
Пример 3. Перевести обыкновенную дробь в десятичную дробь.
Записываем 0 и стáвим запятую:
0,
Теперь посчитаем количество нулей в знаменателе дроби . Видим, что там пять нулей, а в числителе только одна цифра. Чтобы сделать количество нулей в знаменателе и количество цифр в числителе одинаковым, нужно в числителе перед цифрой 5 дописать четыре нуля:
Теперь можно продолжить десятичную дробь. Записываем после запятой числитель дроби
0,00005
В полученной десятичной дроби 0,00005 количество цифр после запятой и количество нулей в знаменателе дроби одинаково. Значит дробь переведена правильно.
Десятичная дробь 0,00005 читается так:
«Ноль целых, пять стотысячных».
Как перевести десятичную дробь в обыкновенную?
Выполним поэтапный перевод:
- Для начала вспомним, что у десятичной дроби есть знаменатель, его просто не пишут. Но зато на знаменатель указывает количество знаков после запятой. Первым шагом мы просто считаем знаки. После чего возводим 10 в получившееся число. Так мы узнали знаменатель будущей обыкновенной дроби.
0,0025 – 4 знака после запятой, значит в знаменателе будет число 10000
Второй шаг – узнать числитель. Для этого нужно убрать все нули и запятые слева от числа. То есть в нашем случае:
25 – такую процедуру называют отбрасыванием запятой.
Третий шаг это запись и сокращение получившейся дроби.
Второй способ перевода
Второй способ более сложный, но применяется чаще первого. Для того, чтобы его использовать нужно вспомнить деление уголком.
Чтобы перевести обыкновенную дробь в десятичную, нужно числитель разделить на знаменатель.
Убеждаемся, что дробь можно перевести в конечную десятичную.
Делим уголком числитель на знаменатель.
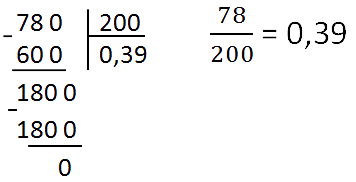
Ниже приведен список дробей со знаменателями, которые чаще других встречаются в заданиях. Вы облегчите себе работу, если их просто выучите.
В данной публикации мы рассмотрим, каким образом обыкновенную (простую) дробь можно перевести в десятичную (конечную и бесконечную). Также разберем решение примеров для лучшего понимания изложенного материала.
- Преобразование обыкновенной дроби в десятичную
- Способ 1
- Способ 2
Перевод десятичных дробей в обыкновенные дроби
Теперь пришло время рассмотреть обратный процесс перевода десятичной дроби в обыкновенную. Сформулируем правило перевода, которое включает три этапа. Как перевести десятичную дробь в обыкновенную?
Правило перевода десятичных дробей в обыкновенные дроби
- В числитель записываем число из исходной десятичной дроби, отбросив запятую и все нули слева, если они есть.
- В знаменатель записываем единицу и за ней столько нулей, сколько цифр есть в исходной десятичной дроби после запятой.
- При необходимости сокращаем полученную обыкновенную дробь.
Рассмотрим применение данного правила на примерах.
Пример 8. Перевод десятичных дробей в обыкновенные
Представим число 3,025 в виде обыкновенной дроби.
- В числитель записываем саму десятичную дробь, отбросив запятую: 3025.
- В знаменателе пишем единицу, а после нее три нуля — именно столько цифр содержится в исходной дроби после запятой: 30251000.
- Полученную дробь 30251000 можно сократить на 25, в результате чего мы получим: 30251000=12140.
Пример 9. Перевод десятичных дробей в обыкновенные
Переведем дробь ,0017 из десятичных в обыкновенные.
- В числителе запишем дробь ,0017, отбросив запятую и нули слева. Получится 17.
- В знаменатель записываем единицу, а после нее пишем четыре нуля: 1710000. Данная дробь несократима.
Если в десятичной дроби есть целая часть, то такую дробь можно сразу перевести в смешанное число. Как это сделать?
Сформулируем еще одно правило.
Правило перевода десятичных дробей в смешанные числа.
- Число, стоящее в дроби до запятой, записываем как целая часть смешанного числа.
- В числителе записываем число, стоящее в дроби после запятой, отбросив нули слева, если они есть.
- В знаменателе дробной части дописываем единицу и столько нулей, сколько цифр есть в дробной части после запятой.
Обратимся к примеру
Пример 10. Перевод десятичной дроби в смешанное число
Представим дробь 155,06005 в виде смешанного числа.
- Записываем число 155, как целую часть.
- В числителе записываем цифры после запятой, отбросив нуль.
- В знаменателе записываем единицу и пять нулей
Поучаем смешанное число: 1556005100000
Дробную часть можно сократить на 5. Сокращаем, и получаем финальный результат:
155,06005=155120120000
Перевод бесконечных периодических десятичных дробей в обыкновенные дроби
Разберем на примерах, как осуществлять перевод периодических десятичных дробей в обыкновенные. Прежде чем начать, уточним: любую периодическую десятичную дробь можно перевести в обыкновенную.
Самый простой случай — период дроби равен нулю. Периодическая дробь с нулевым периодом заменяется на конечную десятичную дробь, а процесс обращения такой дроби сводится к обращению конечной десятичной дроби.
Пример 11. Перевод периодической десятичной дроби в обыкновенную
Обратим периодическую дробь 3,75().
Отбросив нули справа, получим конечную десятичную дробь 3,75.
Обращая данную дробь в обыкновенную по алгоритму, разобранному в предыдущих пунктах, получаем:
3,75()=3,75=375100=154.
Как быть, если период дроби отличен от нуля? Периодическую часть следует рассматривать как сумму членов геометрический прогрессии, которая убывает. Поясним это на примере:
,(74)=,74+,0074+,000074+,00000074+..
Для суммы членов бесконечной убывающей геометрической прогрессии существует формула. Если первый член прогрессии равен b, а знаменатель q таков, что <q<1, то сумма равна b1-q.
Рассмотрим несколько примеров с применением данной формулы.
Пример 12. Перевод периодической десятичной дроби в обыкновенную
Пусть у нас есть периодическая дробь ,(8) и нам нужно перевести ее в обыкновенную.
Запишем:
,(8)=,8+,08+,008+..
Здесь мы имеем бесконечную убывающую геометрическую прогрессию с первым членом ,8 и знаменателем ,1.
Применим формулу:
,(8)=,8+,08+,008+..=,81-,1=,8,9=89
Это и есть искомая обыкновенная дробь.
Для закрепления материала рассмотрим еще один пример.
Пример 13. Перевод периодической десятичной дроби в обыкновенную
Обратим дробь ,43(18).
Сначала записываем дробь в виде бесконечной суммы:
,43(18)=,43+(,0018+,000018+,00000018..)
Рассмотрим слагаемые в скобках. Эту геометрическую прогрессию можно представить в следующем виде:
,0018+,000018+,00000018..=,00181-,01=,0018,99=189900.
Полученное прибавляем к конечной дроби ,43=43100 и получаем результат:
,43(18)=43100+189900
После сложения данных дробей и сокращения получим окончательный ответ:
,43(18)=1944
В завершение данной статьи скажем, что непериодические бесконечный десятичные дроби нельзя перевести в вид обыкновенных дробей.
Всё ещё сложно?
Наши эксперты помогут разобраться
Все услуги
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Перевод периодической дроби в обыкновенную
Давайте разберемся, как перевести периодическую десятичную дробь в обыкновенную дробь.
Если период дроби равен нулю, значит решение будет быстрым. Периодическая дробь с нулевым периодом заменяется на конечную десятичную дробь, а процесс обращения такой дроби сводится к обращению конечной десятичной дроби.
Пример. Преобразуем периодическую дробь 1,32(0) в обыкновенную.
Для этого отбросим нули справа и получим конечную десятичную дробь 1,32. Далее следуем алгоритму из предыдущих пунктов:
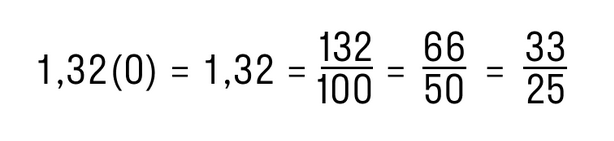
Вот и ответ!
Рассмотрим пример, в котором период дроби отличен от нуля.
Как записать периодическую дробь 10,0219(37) в виде обыкновенной:
- Считаем количество цифр в периоде десятичной дроби. Обозначаем количество цифр за букву k.
В нашем примере k = 2.
- Считаем количество цифр, которые стоят после запятой, но до периода десятичной дроби. Обозначаем количество цифр буквой m.
m = 4.
- Запишем все цифры после запятой: в том числе и цифры из периода в виде натурального числа.
Если вначале, до первой значащей цифры, идут нули, то отбрасываем их. Обозначим полученное число — a.
a = 021937 = 21 937
- Теперь запишем все цифры, которые стоят после запятой, но до периода, в виде натурального числа. Если вначале до первой значащей цифры идут нули, то отбрасываем их. Обозначим полученное число — b.
b = 0219 = 219
- Подставляем найденные значения в формулу, где Y — целая часть бесконечной периодической дроби.
Y = 10
Теперь осталось подставить все найденные значения в формулу и получить ответ:

Вот так мы справились с задачей представить бесконечную периодическую дробь в виде обыкновенной.
Есть еще один способ преобразовать периодическую дробь в обыкновенную. Для этого нужно рассматреть периодическую часть как сумму членов геометрический прогрессии, которая убывает. Например, вот так:
0,(98) = 0,98 + 0,0098 + 0,000098 + 0,00000098 + ..
Для суммы членов бесконечной убывающей геометрической прогрессии есть формула. Если первый член прогрессии равен b, а знаменатель q таков, что 0 < q < 1, то сумма равна b/(1-q).
Пример. Перевести периодическую дробь 0,(7) в обыкновенную.
Как решаем:
- Запишем 0,(7) = 0,7 + 0,07 + 0,007 + ..
Видим бесконечную убывающую геометрическую прогрессию с первым членом 0,7 и знаменателем 0,1.
- Применим формулу b/(1-q):
0,(7) = 0,7 + 0,07 + 0,007 + .. = 0,7 / (1 — 0,1) = 0,7/0,9 = 7/9.
Ответ: 7/9.
Итак, есть два вида периодических дробей. Сейчас расскажем, чем отличаются способы их преобразования в обыкновенные дроби.
Определение периодической дроби
Периодическая дробь — это бесконечная десятичная дробь, в которой, начиная с некоторого места, периодически повторяется определенная группа цифр.
Периодическая часть дроби — это набор повторяющихся цифр, из которых состоит значащая часть.
В краткой записи периодической дроби повторяющиеся цифры пишут в скобках и называют периодом дроби. Например, вместо 1,555… записывают 1,(5) и читают «одна целая и пять в периоде».
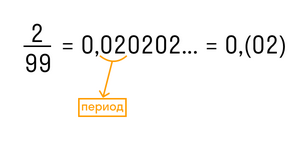
Остальной отрезок значащей части, который не повторяется, называется непериодической частью.
Виды периодических дробей: чистые и смешанные.
Чистая периодическая десятичная дробь — это десятичная дробь, в записи которой сразу после запятой следует период. Например: 1,(4); 4,(25); 21,(693).
Смешанная периодическая десятичная дробь — это десятичная дробь, в записи которой после запятой через одну или несколько цифр начинается период. Например: 3,5(1); 0,02(89); 7,0(123) и т.д.
Рассмотрим примеры дробей, чтобы научиться определять части и период.
1/3 = 0,3333… = 0,(3)
Непериодическая часть: 0; периодическая часть: 3; длина периода: 1.
Читаем так: ноль целых три в периоде.
7/12 = 0,583333… = 0,58(3)
Непериодическая часть: 0,58; периодическая часть: 3; длина периода: снова 1.
Читаем так: ноль целых пятьдесят восемь сотых и три в периоде.
17/11 = 1,545454… = 1,(54)
Непериодическая часть: 1; периодическая часть: 54; длина периода: 2.
Читаем так: одна целая пятьдесят четыре сотых в периоде.
25/39 = 0,641025 641025… = 0,(641025)
Непериодическая часть: 0; периодическая часть: 641025; длина периода: 6.
Читаем так: ноль целых шестьсот сорок одна двадцать пять миллионных в периоде.
пятьдесят четыре сотых в периоде.
9200/3 = 3066,666… = 3066,(6)
Непериодическая часть: 3066; периодическая часть: 6; длина периода: 1.
Читаем так: три тысячи шестьдесят шесть целых и шесть в периоде.
Определение дроби
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.
Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:
- обыкновенный вид — ½ или a/b,
- десятичный вид — 0,5.
В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.
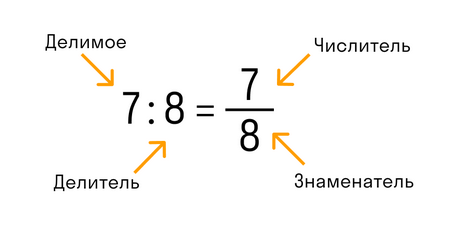
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
- 0,7
- 6,51
- 9,932
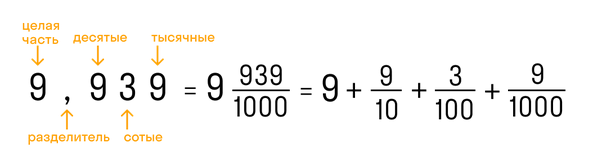
Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.

Как перевести периодическую десятичную дробь в обыкновенную
Любую бесконечную периодическую десятичную дробь можно перевести в обыкновенную. Разберем на примерах.
Если период дроби равен нулю, значит решение будет быстрым. Периодическая дробь с нулевым периодом заменяется на конечную десятичную дробь, а процесс обращения такой дроби сводится к обращению конечной десятичной дроби.
Преобразуем периодическую дробь 1,32(0) в обыкновенную.
Для этого отбросим нули справа и получим конечную десятичную дробь 1,32. Далее следуем алгоритму из предыдущих пунктов:
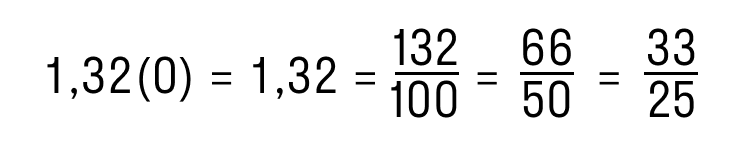
Вот и ответ!
Если период дроби отличен от нуля — рассматриваем периодическую часть как сумму членов геометрический прогрессии, которая убывает. Поясним на примере:
0,(98) = 0,98 + 0,0098 + 0,000098 + 0,00000098 + ..
Для суммы членов бесконечной убывающей геометрической прогрессии есть формула. Если первый член прогрессии равен b, а знаменатель q таков, что 0 < q < 1, то сумма равна b/(1-q).
Переведем периодическую дробь 0,(7) в обыкновенную.
Запишем: 0,(7) = 0,7 + 0,07 + 0,007 + .. Видим бесконечную убывающую геометрическую прогрессию с первым членом 0,7 и знаменателем 0,1. Применим формулу: 0,(7) = 0,7 + 0,07 + 0,007 + .. = 0,7 / (1 — 0,1) = 0,7/0,9 = 7/9.
Правило перевода десятичной дроби в обыкновенную
Чтобы перевести десятичную дробь в простую, придерживаемся следующих правил:
1. Целая часть десятичной дроби – это то же самое, что и целая часть обыкновенной дроби, которая в данном случае будет являться смешанной.Примечание: если целая часть десятичной дроби равняется нулю, значит мы имеем дело с правильной простой дробью (числитель меньше знаменателя).
2. Цифры после запятой (дробная часть) в десятичной дроби пишем в числителе дробной части обыкновенной дроби. При этом, отбрасываем все нули.
3. В знаменателе дробной части простой дроби пишем единицу и количество нулей, равное количеству цифр после запятой в десятичной дроби.Примечание: Нули, которые иногда могут встречаться после цифр в дробной части десятичной дроби, не считаются (согласно основному свойству) и их можно отбросить.
Чтобы превратить бесконечную десятичную дробь в обыкновенную сначала ее следует округлить и только после этого выполнить перевод.
Для перевода бесконечных периодических десятичных дробей в простые дроби есть отдельная инструкция.
Понятие десятичной дроби
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.
Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:
- обыкновенный вид — ½ или a/b,
- десятичный вид — 0,5.
В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
- 0,8
- 7,42
- 9,932
Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Более быстрый способ
В данном алгоритме также 3 шага. Чтобы получить обычную дробь из десятичной, нужно выполнить следующее:
Вот и всё! На первый взгляд, эта схема сложнее предыдущей. Но на самом деле он и проще, и быстрее. Судите сами:
Как видим, в дроби 0,64 после запятой стоит две цифры — 6 и 4. Поэтому $n=2$. Если убрать запятую и нули слева (в данном случае — всего один ноль), то получим число 64. Переходим ко второму шагу: $^>=^>=100$, поэтому в знаменателе стоит именно сто. Ну а затем остаётся лишь сократить числитель и знаменатель.:)
Ещё один пример:
Здесь всё чуть сложнее. Во-первых, цифр после запятой уже 3 штуки, т.е. $n=3$, поэтому делить придётся на $^>=^>=1000$. Во-вторых, если убрать из десятичной записи запятую, то мы получим вот это: 0,004 → 0004. Вспомним, что нули слева надо убрать, поэтому по факту у нас число 4. Дальше всё просто: делим, сокращаем и получаем ответ.
Наконец, последний пример:
Особенность этой дроби — наличие целой части. Поэтому на выходе у нас получается неправильная дробь 47/25. Можно, конечно, попытаться разделить 47 на 25 с остатком и таким образом вновь выделить целую часть. Но зачем усложнять себе жизнь, если это можно сделать ещё на этапе преобразований? Что ж, разберёмся.
Что такое десятичная дробь
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
- 0,8
- 7,42
- 9,932
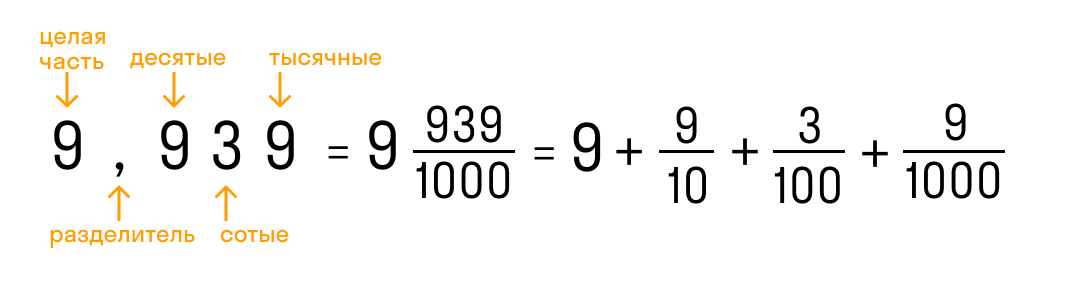
Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
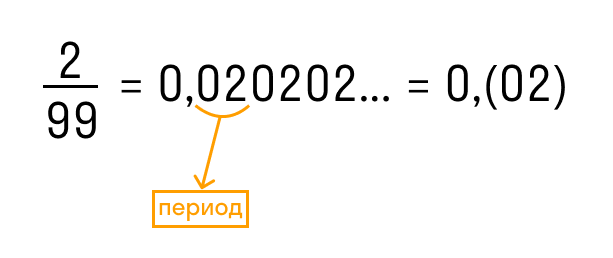
В краткой записи периодической дроби повторяющиеся цифры пишут в скобках и называют периодом дроби. Например, вместо 1,555… записывают 1,(5) и читают «одна целая и пять в периоде».
Что такое дробь?
Для начала вспомним, что такое обыкновенная дробь. Это число, которое обозначает часть единицы, чего-то целого. Для того, чтобы использовать подобные числа в расчетах, нам нужно знать, на сколько частей поделили единицу и сколько частей мы взяли для расчета.
Например, вы решаете задачу, где сказано, что папа съел одну четвертую часть пирога. Нужно посчитать, сколько калорий употребил папа. В этом случае, для расчета нам потребуется дробь, которая обозначит часть пирога. Значит, пирог – это целое. На сколько частей поделили пирог?
Дробь записывается в виде двух чисел, разделенных чертой. Верхнее число зовется числителем. Как раз оно и отображает количество съеденных кусков. Тогда как знаменатель, это общее количество кусочков, на которое разделили целое.
Если числитель и знаменатель равны, то никакой дроби не получится. Получится число: 1. Так же, если числитель является кратным для знаменателя, то дробь сразу сокращают до целого числа.
Как превратить десятичную дробь в обычную?
Например, 3,45 или 0,299.Например: \( \frac{4}{5} \), \( \frac{25}{70} \), 3\( \frac{2}{7} \)
Первый способ – механический
\( \frac{1}{20} \)
- Запишем в числитель значимые цифры ДД (без нулей слева и запятых), а в знаменатель – единицу: \( \frac{5}{1} \).
- Добавим к единице столько нулей, сколько знаков после запятой в исходном числе 0,05, то есть два: \( \frac{5}{100} \).
- Сократим получившуюся ОД на 5, получим \( \frac{1}{20} \).
Результат решения: \( \frac{5}{100} \)\( \frac{1}{20} \)
- Запишем в числитель все цифры без запятой: \( \frac{3075}{} \).
- В знаменатель – “1” и столько “0”, сколько знаков после запятой в числе 3,075 – три: \( \frac{3075}{1000} \).
- Сократим на 25: \( \frac{3075}{1000} \)= \( \frac{123}{40} \) (можно постепенно, два раза по 5).
- Если далее следуют еще какие-то вычисления, можно оставить ее в таком виде. Если нет, превратим неправильную дробь в правильную, выделив целую часть, 123 : 40 = 3 (и 3 в остатке). Значит — \( \frac{123}{40} \) = 3\( \frac{3}{40} \)
Ход преобразований: \( \frac{3075}{1000} \) \( \frac{123}{40} \)\( \frac{3}{40} \)
- Оставляем целое ДД “за кадром” и займемся только дробным компонентом: 3,075 – это 3 + 0,075:
- 3 пока не трогаем;
- 0,075 переводим в ОД: \( \frac{75}{1000} \).
- Сокращаем полученную дробь на 25: \( \frac{75}{1000} \) = \( \frac{3}{40} \).
- Возвращаем целую часть на свое место, соединяем: 3,075 = 3\( \frac{3}{40} \).
Вся последовательность: \( \frac{75}{1000} \)\( \frac{3}{40} \)\( \frac{3}{40} \)
Второй способ – “на слух”
- восемь/девятых – \( \frac{8}{9} \);
- одиннадцать/тридцатых – \( \frac{11}{30} \);
- сто две/триста семнадцатых – \( \frac{102}{317} \).
например, 0,45:
- 0, 45 – это (слушаем!) сорок пять/сотых – \( \frac{45}{100} \);
- Теперь сократим на 5: \( \frac{45}{100} \) = \( \frac{9}{20} \).
В итоге получаем: \( \frac{45}{100} \)\( \frac{9}{20} \)14,408 в виде ОД:
- 14 целых не трогаем. Превращаем: 0,408 = \( \frac{408}{1000} \).
- Сокращаем на 8: \( \frac{408}{1000} \) = \( \frac{51}{125} \).
- Соединяем целую и дробную части.
Ход решения: \( \frac{408}{1000} \)\( \frac{51}{125} \)
Еще несколько примеров:
- 1, 08 – одна целая, восемь сотых – 1\( \frac{8}{100} \) = 1\( \frac{2}{25} \) (дробную составляющую уменьшили в 4 раза);
- 5,0125 – пять целых, сто двадцать пять/десятитысячных – 5\( \frac{125}{1000} \) = 5\( \frac{1}{80} \) (сократили на 125);
- 0,648 – шестьсот сорок восемь тысячных – \( \frac{648}{1000} \) = \( \frac{81}{125} \) (разделили все на 8).






