Объем прямоугольного параллелепипеда
Давайте вспомним, какие виды параллелепипедов бывают.
Параллелепипедом называется призма, основаниями которой являются параллелограммы. Другими словами, параллелепипед — это многогранник с шестью гранями. Каждая грань которой называется параллелограмм.
Призма — это многогранник, в основаниях которого лежат равные многоугольники, а его боковые грани — это параллелограммы.
Какие бывают призмы:
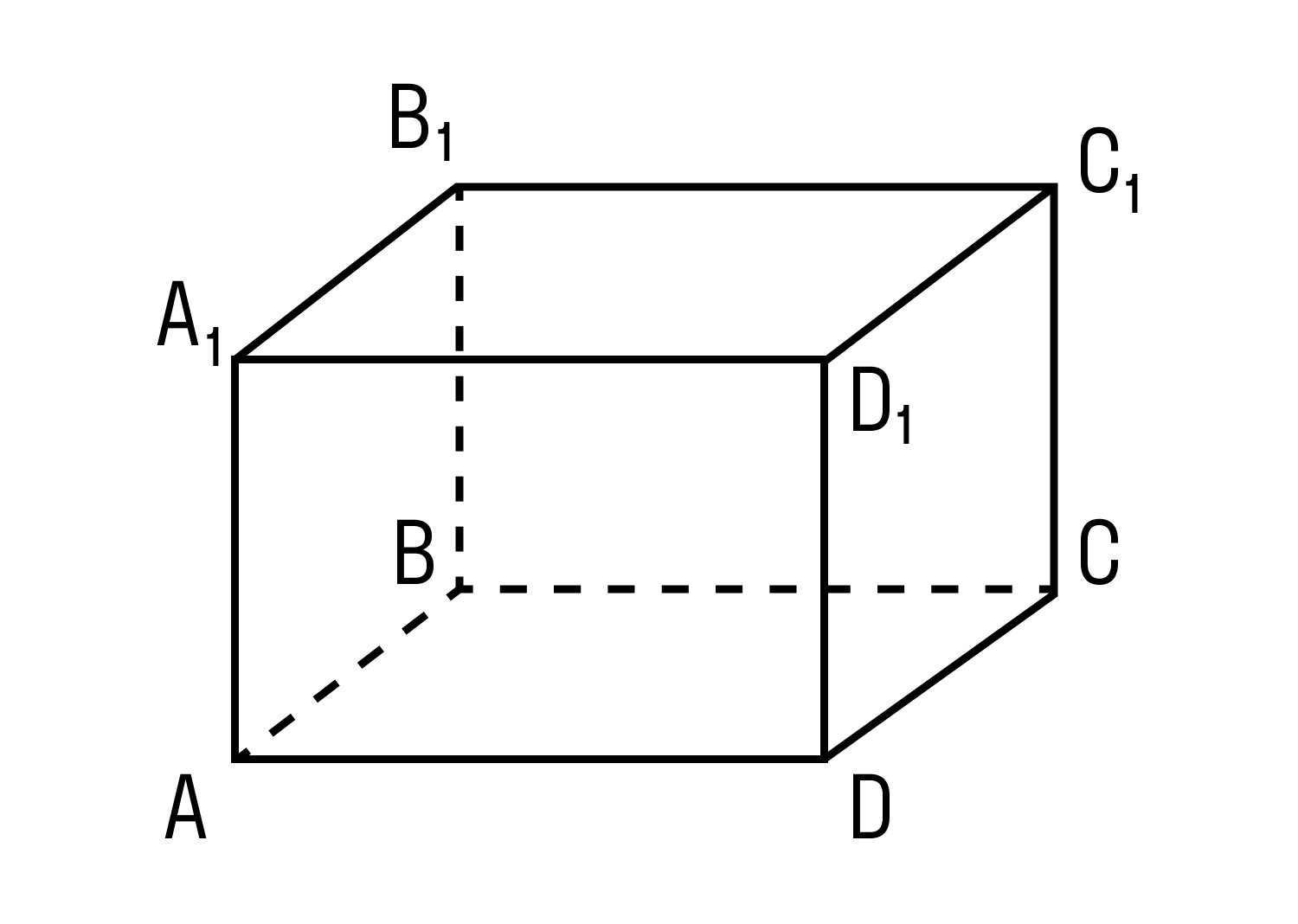
Прямой параллелепипед — это параллелепипед, у которого боковые ребра перпендикулярны основанию.
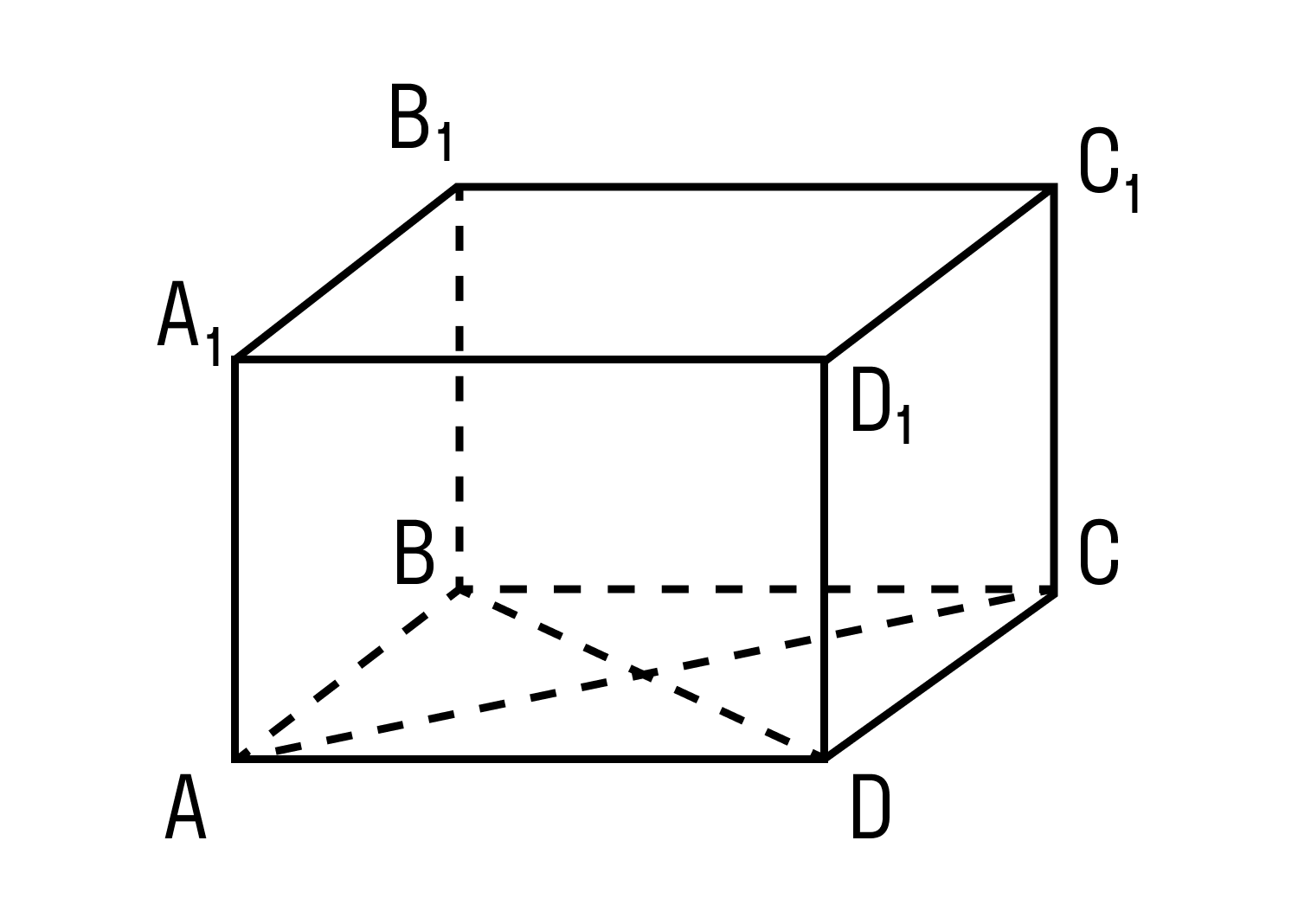
Прямоугольным параллелепипедом называют параллелепипед, у которого основание — прямоугольник, а боковые ребра перпендикулярны основанию.
|
Формула объема прямоугольного параллелепипеда Чтобы вычислить объем прямоугольного параллелепипеда, найдите произведение его длины, ширины и высоты: V = a * b * h |
Чтобы не запутаться в формулах, запоминайте табличку с условными обозначениями.
|
a |
длина параллелепипеда |
|
b |
ширина параллелепипеда |
|
h |
высота параллелепипеда |
|
P (осн) |
периметр основания |
|
S (осн) |
площадь основания |
|
S (бок) |
площадь боковой поверхности |
|
S (п.п.) |
площадь полной поверхности |
|
V |
объем |
Пример 1. Чему равен объем параллелепипеда со сторонами 9 см, 6 см, 3 см.
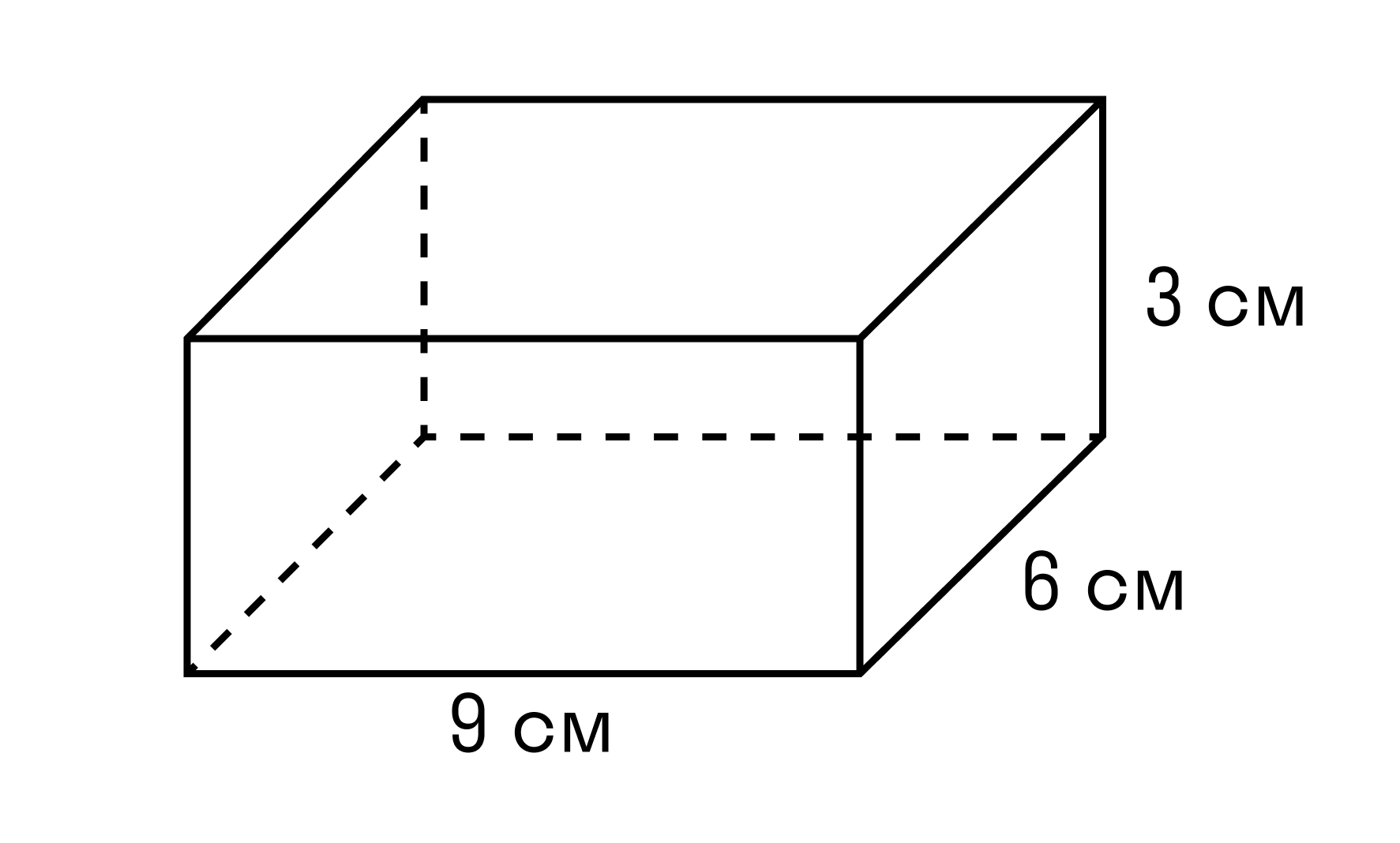
a = 9 см
b = 6 см
h = 3 см
V = a * b * h
V = 9 * 6 * 3 = 162 см3.
Ответ: объем прямоугольного параллелепипеда равен 162 см3.
|
Следствие 1 Объем параллелепипеда равен произведению площади основания на высоту. V = S осн * h |
Из этого следствия выведем формулу нахождения площади основания параллелепипеда.
S осн = V : h
Пример 2. Найдите площадь основания параллелепипеда, если его объем равен 82 см3, а высота 8 см.
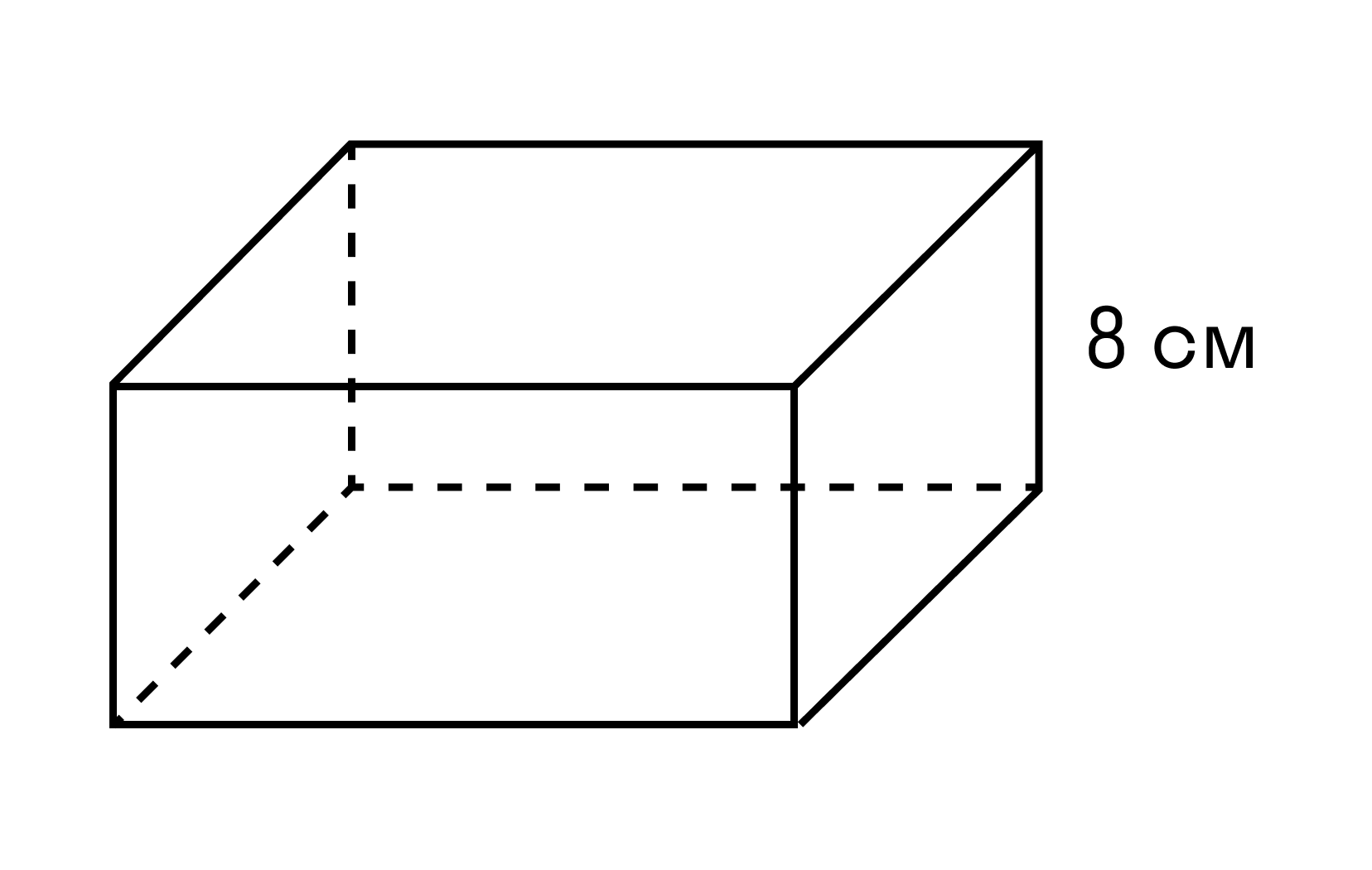
V = 82 см3
h = 8 см
V = S осн * h
S осн = V : h
S осн = 82 см3: 8 см = 10,25 см2.
Ответ: площадь основания параллелепипеда равна 10,25 см2.
|
Следствие 2 Объём прямой призмы, основанием которой является прямоугольный треугольник, равен произведению площади основания на высоту. V = S осн * h |
Пример 3. Основанием прямой призмы служит прямоугольный треугольник с катетами 6 и 8 см. Боковое ребро равно 5. Найдем объем призмы.
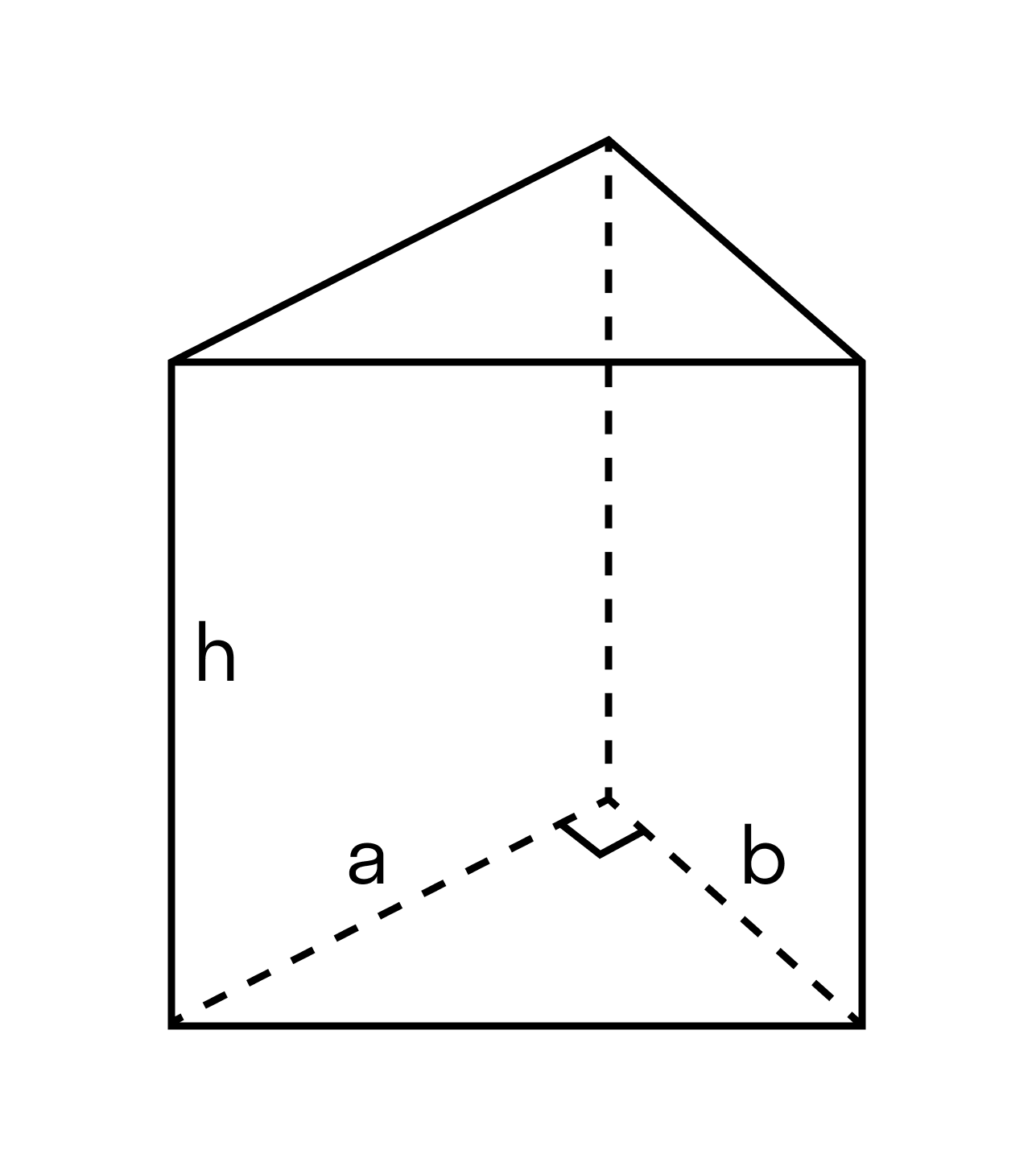
V = S * h = 12* a * b * h
a = 6
b = 8
h = 5
V = 1/2 * 6 * 8 * 5 = 120 см3.
Ответ: объём прямой призмы, основанием которой является прямоугольный треугольник, равен 120 см3.
Решение примеров
Несмотря на то что формулы довольно простые, запомнить их простой зубрёжкой сложно. Чтобы материал закрепился, нужно научиться их применять на практике. Если понять принцип нахождения длины, многие из этих выражений можно будет вывести самостоятельно.
Вот некоторые задачи, рассчитанные на учащихся седьмых классов, рекомендуемые к самостоятельной проработке:

- Определить длину прямоугольного многоугольника, у которого длина в 4 раза больше ширины. Периметр тела равен 20 см. Для решения задачи нужно принять сторону фигуры за х. Тогда длина будет составлять 4х. Согласно формуле, периметр равен: P = 2AB + 2 BC = 2* x + 2 * 4x. После подстановки значения P и выражения неизвестного, должно получиться следующее равенство: x = 20 / 10 = 2. Отсюда следует, что искомая длина равняется: BC = 4 * x = 4 * 2 = 8 см. Задача решена.
- Длина прямоугольной фигуры больше её ширины на 2. Если ширина увеличится на 3 см, а длина на 8, площадь фигуры возрастёт в 3 раза. Найти длину. Чтобы решить задачу, нужно рассуждать следующим образом: пусть x ширина для первого состояния фигуры. Значит, длина этой фигуры будет x + 2. Соответственно, площадь равна: S = x * (x + 2). После трансформации ширина изменилась до значения x + 3, а длина — х + 2 + 8 = х + 10. Площадь новой фигуры равна: S = (х + 3) * (х + 10). После раскрытия скобок получится уравнение: 2 * х2 — 7* х — 30 = 0. После его решения должно получиться, что x = 6 см. Отсюда длина будет равняться: 6 + 2 = 8 см.
- Определить длину и ширину прямоугольника ABCD, в который вписаны 3 круга, если радиус каждой описанной окружности равен 5 см. Для решения примера нужно вспомнить, что ширина многоугольника равна двум радиусам круга или его диаметру. Значит, AB = 2 * 5 = 10 см. Соответственно, длина будет составлять 3 диаметра или 6 радиусов: BC = 6 * 5 = 30 см. Ответ найден.
В процессе изучения материала совсем не зазорно пользоваться так называемыми онлайн-калькуляторами. Это сайты, предлагающие своим пользователям рассчитать различные математические величины по исходным данным. Их интересность не только в том, что можно получить готовый ответ, но и в появлении возможности просмотреть подробное решение. Это как раз и позволит устранить пробелы в знании на стадии обучения.
Объём геометрической фигуры
Объём геометрической фигуры — это число, которое характеризует вместимость данной фигуры.
Объём измеряется в кубических единицах. Под кубическими единицами подразумевают кубы длиной 1, шириной 1 и высотой 1. Например, 1 кубический сантиметр или 1 кубический метр.
Измерить объём какой-нибудь фигуры означает выяснить сколько кубических единиц вмещается в данную фигуру.
Например, объём следующего прямоугольного параллелепипеда равен двенадцати кубическим сантиметрам:
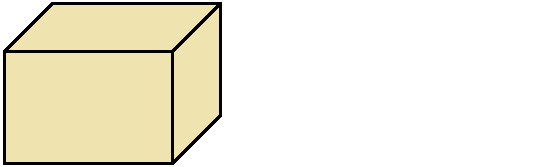
Это потому что в данный параллелепипед вмещается двенадцать кубов длиной 1 см, шириной 1 см и высотой 1 см:
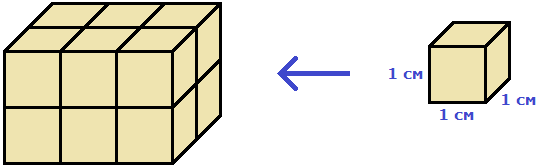
Объём обозначается заглавной латинской буквой V. Одна из единиц измерения объема это кубический сантиметр (см3). Тогда объём V рассмотренного нами параллелепипеда равен 12 см3
V = 12 см3
Объём любого параллелепипеда вычисляют следующим образом: перемножают его длину, ширину и высоту .
Объём прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.
V = abc
где, a — длина, b — ширина, c — высота
Так, в предыдущем примере мы визуально определили, что объём параллелепипеда равен 12 см3. Но можно измерить длину, ширину и высоту данного параллелепипеда и перемножить результаты измерений. Мы получим тот же результат
Объём куба вычисляется таким же образом, как и объём прямоугольного параллелепипеда — перемножают длину, ширину и высоту.
Например, вычислим объём куба, длина которого 3 см. У куба длина, ширина и высота равны между собой. Если длина равна 3 см, то равны этим же трём сантиметрам ширина и высота куба:
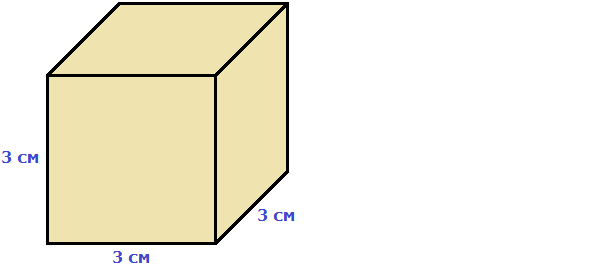
Перемножаем длину, ширину, высоту и получаем объём, равный двадцати семи кубическим сантиметрам:
V = 3 × 3 × 3 = 27 см³
Действительно, в исходный куб вмещается 27 кубиков длиной 1 см
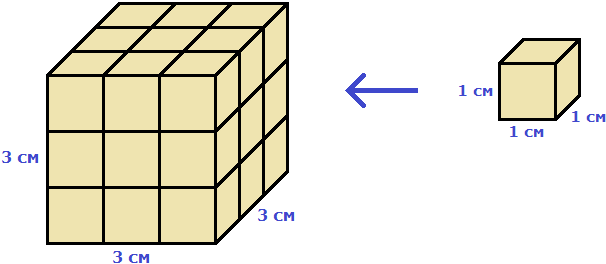
При вычислении объёма данного куба мы перемножили длину, ширину и высоту. Получилось произведение 3 × 3 × 3. Это есть произведение трёх сомножителей, каждый из которых равен 3. Иными словами, произведение 3 × 3 × 3 является третьей степенью числа 3 и может быть записано в виде 33.
V = 33 = 27 см3
Поэтому третью степень числа называют кубом числа. При вычислении третьей степени числа a, человек тем самым находит объём куба, длиной a. Операцию возведения числа в третью степень по другому называют возведением в куб.
Таким образом, объём куба вычисляется по следующему правилу:
V = a3
Где a — длина куба.
Кубический дециметр. Кубический метр
Не все объекты нашего мира удобно измерять в кубических сантиметрах. Например, объём комнаты или дома удобнее измерять в кубических метрах (м3). А объём бака, аквариума или холодильника удобнее измерять в кубических дециметрах (дм3).
Другое название одного кубического дециметра – один литр.
1 дм3 = 1 литр
Периметр прямоугольника
Определение.
Периметром прямоугольника
Формулы определения длины периметру прямоугольника
1. Формула периметру прямоугольника через две стороны прямоугольника:
P = 2a
+ 2b
P = 2(a
+ b
)
2. Формула периметру прямоугольника через площадь и любую сторону:
| P = | 2S + 2a 2 |
= | 2S + 2b 2 |
|
a |
b |
3. Формула периметру прямоугольника через диагональ и любую сторону:
P = 2(a
+ √d
2 — a
2
) = 2(b
+ √d
2 — b
2
)
4. Формула периметру прямоугольника через радиус описанной окружности и любую сторону:
P = 2(a
+ √4R 2 — a
2
) = 2(b
+ √4R 2 — b
2
)
5. Формула периметру прямоугольника через диаметр описанной окружности и любую сторону:
P = 2(a
+ √D o 2 — a
2
) = 2(b
+ √D o 2 — b
2
)
Как выбрать оптимальную диагональ телевизора?
Диагональ экрана телевизора – относительно самостоятельная характеристика, не зависящая от других параметров устройства. Современный электронный рынок – прямое тому подтверждение. Так, например, сегодня можно легко найти модели с относительно небольшой диагональю и высоким разрешением или, наоборот, с низким разрешением и большой диагональю. Однако этот факт не означает, что при выборе новой ТВ-панели нужно ориентироваться исключительно на размер дисплея. Комфортность просмотра, качество изображения и детализация зависят от соотношения диагонали, разрешения и сторон монитора.
Для выбора оптимальной модели телевизора рекомендуем придерживаться следующих правил:
Чем больше диагональ телевизора, тем выше должно быть разрешение экрана. Дело в том, что на больших телевизионных панелях легко можно увидеть любые изъяны и изъяны отображаемого изображения.
Чем меньше соотношение сторон, тем меньше диагональ экрана. В случае, если речь идет об огромном телевизоре с соотношением сторон 4: 3, большая площадь монитора будет «съедена» черными кадрами
Чем больше комната, тем больше диагональ и наоборот, чем меньше комната, тем меньше диагональ. Вот простое правило. Так, например, если речь идет о маленькой кухне, оптимальным вариантом будет компактный 19-22-дюймовый монитор
Если покупатель планирует оборудовать полноценный домашний кинотеатр в большой гостиной, есть смысл обратить внимание на современные жидкокристаллические панели с диагональю от 90 дюймов и более.
Для стандартных комнат площадью 16-20 квадратов оптимальным параметром экрана будет 32-40 дюймов с соотношением сторон 16: 9 и разрешением 1920 * 1080. Если монитор меньше, зрители их не увидят сможете в полной мере насладиться резкостью и качеством изображения. Если вы купите телевизор размером более 40 дюймов, глаза тех, кто находится в комнате, начнут уставать в течение 40-60 минут после просмотра любимого фильма
В любом случае, выбирая оптимальную диагональ телевизора, в первую очередь нужно обращать внимание на свои вкусы, потребности, иначе дорогая покупка не принесет радости
Прямая и обратная пропорциональность
Давайте сначала разберемся, что такое пропорциональность.
Пропорциональность — это зависимость двух величин друг от друга таким образом, что значение отношения этих величин остается постоянным.
Зависимость величин друг от друга может быть прямой и обратной.
Отношение между величинами описываются прямой или обратной пропорциональностью.
Прямая пропорциональность выражается так: (mathbf)
Обратная пропорциональность выражается так: (mathbf>)
где k — это число, которое называют коэффициентом пропорциональности.
x и y величины, зависящие друг от друга.
Пример
Площадь прямоугольника равна (mathbf), где S— это площадь прямоугольника, а — длина прямоугольника, b — ширина прямоугольника.
Если один из множителей произведения — постоянная величина, то произведение прямо пропорционально второму множителю.
Если постоянно значение произведения, то множители зависят друг от друга обратно пропорционально.
По формуле видно, что площадь квадрата зависит от длины (ширины) его стороны, а длина стороны (ширина) зависит от его площади.
Какова эта зависимость, сейчас и рассмотрим.
Зависимость площади прямоугольника от длины при постоянном значении ширины является прямо пропорциональной зависимостью этих величин.
Зависимость площади прямоугольника от ширины при постоянном значении длины является прямо пропорциональной зависимостью этих величин.
Пусть одна клетка равна 1 см. Рассмотрим рисунок:
Ширина прямоугольника b постоянная величина
b = 4 см
a1 = 6 см
Увеличим ширину прямоугольника — сторону a1 на 1 см, получим
a2 = 7 см
Найдем площади прямоугольников S1 и S2
(mathbf = a_ cdot b = 6 cdot 4 = 24>) см 2
(mathbf = a_ cdot b = 7 cdot 4 = 28>) см 2
Вывод: при увеличении стороны прямоугольника увеличилась площадь прямоугольника.
Рассмотрим другой вариант зависимости
Зависимость одной из сторон прямоугольника от второй стороны при постоянном значении площади прямоугольника является обратно пропорциональной зависимостью. Пусть одна клетка равна 1 см
Площадь прямоугольника S постоянная величина
S = 24 см 2
b1 = 4 см
Увеличим высоту прямоугольника- сторону прямоугольника b1 на 2 см, получим
b2 = 6 см
Найдем ширину прямоугольника- сторону a2
Вывод: при увеличении одной стороны прямоугольника и постоянном значении площади, вторая сторона уменьшается.
Таким образом, мы подошли к основным понятиям пропорциональной зависимости. Чтобы было легко разобраться в несложных схемах ниже, мы дадим пояснение символам:
1) Две величины прямо пропорциональны друг другу, если при увеличении (уменьшении) одной величины в n количество раз, другая величина, зависящая от первой, так же увеличивается (уменьшается) в n количество раз.
2) Две величины обратно пропорциональны друг другу, если при увеличении (уменьшении) одной величины в n количество раз, другая величина, зависящая от первой, уменьшается (увеличивается) в n количество раз.
Примеров прямой и обратной пропорциональности множество.
Однако не все величины зависят друг от друга прямо пропорционально или обратно пропорционально, встречаются и более простые и более сложные зависимости величин.
Надо понимать, что даже если какие-нибудь две величины возрастают или убывают, то между ними не обязательно существует пропорциональная зависимость.
Например, с течением времени увеличивается возраст человека и его размер ноги, но эти величины не являются пропорциональными, так как при удвоении возраста размер ноги человека не удваивается

Пройти тест и получить оценку можно после входа или регистрации
Задачи:
1. Хозяин дачи решил построить забор вокруг участка. Какой длины получится забор, если участок имеет вид прямоугольника с шириной 15 метров и длиной 33 метра?
Решение:
Для нахождения длины забора нужно посчитать периметр участка.
Воспользуемся формулай Ручастка = 2 * (длина + ширина).
Ручастка = 2 * (15 м + 33 м) = 96 м
Ответ: длина забора 96 метров.
2. Мама решила пришить на скатерть красивую тесьму. Сколько нужно купить тесьмы, если скатерть квадратная со стороной 150 сантиметров?
Решение:
Так как скатерть квадратная, для определения длины тесьмы нужно найти периметр квадрата.
Р = 4 * 150 см = 600 см = 6 м
Ответ: нужно купить 6 метров тесьмы.
3. Известно, что банки краски хватает, чтобы покрасить 30 м2 поверхности. Хватит ли одной банки краски, чтобы покрасить забор длиной 15 метров и высотой 2 метра?
Решение:
Для решения необходимо найти площадь поверхности забора. Для этого длину умножаем на ширину.
Sзабора = 15 м * 2 м = 30 м2.
Ответ: да, 1 банки краски хватит.
Варианты нахождения периметра прямоугольника
По сторонам
Если нам известны все стороны прямоугольника (или две смежные), мы можем использовать следующую формулу для нахождения суммы длин всех ребер:
\(P=2(a+b)\)
где \(a\) и \(b\) — это две соседние стороны фигуры.
По любой стороне и площади
Зная значение любого из ребер четырехугольника и его площадь, мы можем найти значение второго и периметр фигуры.
Так как площадь прямоугольника — это произведение двух его смежных сторон \((S=a\times b)\), чтобы найти неизвестную сторону, нужно поделить площадь на известную величину: \(b=\frac Sa\).
Получается, что формула для расчета \(P\) рассматриваемой фигуры будет выглядеть следующим образом:
\(P=2(\frac Sa+a)\)
По любой стороне и диагонали
В случае, если мы знаем длину одного из ребер и диагональ данного четырехугольника, мы можем найти вторую сторону с помощью теоремы Пифагора.
\(b=\sqrt{d^2-a^2}\)
где \(d\) — диагональ прямоугольника, а \(b\) — неизвестная сторона.
Чтобы рассчитать сумму длин всех сторон, нужно воспользоваться формулой:
\(P=2(a+\sqrt{d^2-a^2})\)
По любой стороне и радиусу описанной окружности
Когда нам известна одна из сторон и радиус описанной окружности вокруг прямоугольника, мы можем узнать его неизвестное ребро. Из свойств прямоугольника помним, что точка пересечения диагоналей фигуры — это центр описанной окружности. Это значит, что 1/2 диагонали — это радиус этой окружности. Таким образом, по теореме Пифагора мы можем узнать неизвестную сторону прямоугольника:
\(b=\sqrt{4R^2-a^2}\)
где \(R\) — радиус описанной окружности.
Тогда формула для расчета P будет выглядеть так:
\(P=2(a+\sqrt{4R^2-a^2})\)
Классификация
Прямоугольник — это частный случай параллелограмма и трапеции . Квадрат является частным случаем прямоугольника.
Традиционная иерархия
Прямоугольник является частным случаем параллелограмма , в котором каждая пара смежных сторон находится перпендикулярно .
Параллелограмм — это особый случай трапеции (известной как трапеция в Северной Америке), в которой обе пары противоположных сторон параллельны и равны по длине .
Трапеция — это выпуклый четырехугольник, у которого есть по крайней мере одна пара параллельных противоположных сторон.
Выпуклый четырехугольник — это
- Просто : граница не пересекает саму себя.
- В форме звезды : весь интерьер виден с одной точки, не пересекая края.
Альтернативная иерархия
Де Вильерс определяет прямоугольник в более общем смысле как любой четырехугольник с осями симметрии, проходящими через каждую пару противоположных сторон. Это определение включает как прямоугольные прямоугольники, так и скрещенные прямоугольники. Каждая из них имеет ось симметрии, параллельную и равноудаленной от пары противоположных сторон, а другая — серединный перпендикуляр этих сторон, но в случае скрещенного прямоугольника первая ось не является осью симметрии для обеих сторон. что он делит пополам.
Четырехугольники с двумя осями симметрии, каждая из которых проходит через пару противоположных сторон, относятся к большему классу четырехугольников, по крайней мере, с одной осью симметрии через пару противоположных сторон. Эти четырехугольники состоят из равнобедренных трапеций и скрещенных равнобедренных трапеций (скрещенные четырехугольники с таким же расположением вершин, что и равнобедренные трапеции).
Таблица квадратов
В жизни часто приходиться находить площади различных квадратов. Для этого каждый раз требуется возводить исходное число во вторую степень.
Квадраты первых 99 натуральных чисел уже вычислены и занесены в специальную таблицу, называемую таблицей квадратов.
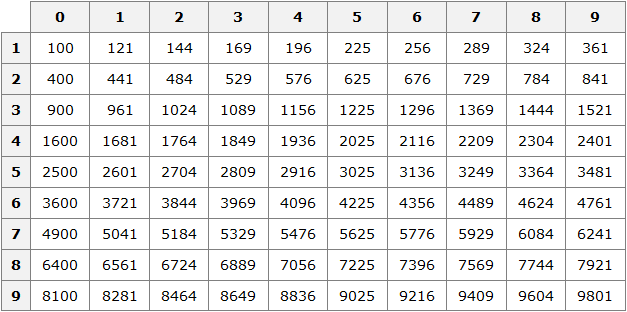
Первая строка данной таблицы (цифры от 0 до 9) это единицы исходного числа, а первый столбец (цифры от 1 до 9) это десятки исходного числа.
Например, найдём квадрат числа 24 по данной таблице. Число 24 состоит из цифр 2 и 4. Точнее, число 24 состоит из двух десятков и четырёх единиц.
Итак, выбираем цифру 2 в первом столбце таблицы (столбце десятков), а цифру 4 выбираем в первой строке (строке единиц). Затем, двигаясь вправо от цифры 2 и вниз от цифры 4, найдём точку пересечения. В результате окажемся на позиции, где располагается число 576. Значит, квадрат числа 24 есть число 576
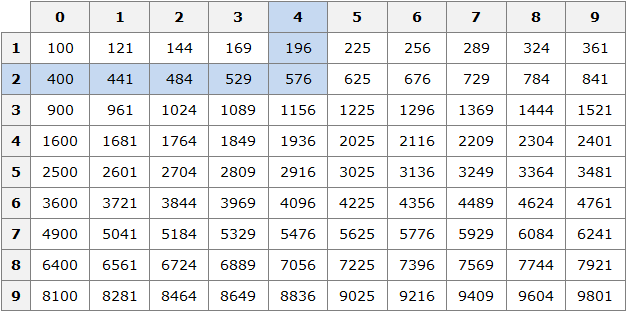
242 = 576
Выравнивание величины прямоугольника
В прямоугольнике все углы должны быть 90 °, иначе получится неравнобедренная фигура с искаженными стенами. Контур фундамента имеет внешнюю и внутреннюю стороны, поэтому требование прямоугольности распространяется на оба контура. Проще всего выровнять значение для простого прямоугольного дома с четырьмя стенами.
Иногда фундамент в плане имеет сложную конструкцию, например, для пристройки или веранды делают дополнительные монолитные ленты, а каминный зал считается самостоятельным помещением. В этом случае разметка усложняется тем, что площадь дома будет состоять из отдельных прямоугольников, размеченных отдельно.
После планирования каждая фигура проверяется на соответствие остальным деталям, а также выставляются прямые углы между составляющими элементами. Исходная сторона прикреплена к основанию, что выглядит просто. Это может быть забор, забор, трамвайный путь или бордюр мощеного пути. Такое же расстояние проводится от этой линии, чтобы указать первую сторону желаемой плоскости фундамента.
После окончательной разметки необходимо правильно рассчитать диагональ и сравнить расстояние между первой-третьей и второй-четвертой вершинами прямоугольника на земле. У вас должны получиться абсолютно равные расстояния. Также проверяется длина противоположных сторон, которая также должна быть одинаковой.
Периметр геометрической фигуры
Периметр геометрической фигуры — это сумма всех её сторон. Чтобы вычислить периметр, нужно измерить каждую сторону и сложить результаты измерений.
Вычислим периметр следующей фигуры:
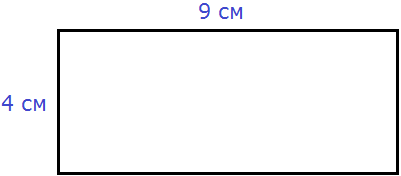
Это прямоугольник. Детальнее мы поговорим об этой фигуре позже. Сейчас просто вычислим периметр этого прямоугольника. Длина его равна 9 см, а ширина 4 см.
У прямоугольника противоположные стороны равны. Это видно на рисунке. Если длина равна 9 см, а ширина равна 4 см, то противоположные стороны будут равны 9 см и 4 см соответственно:
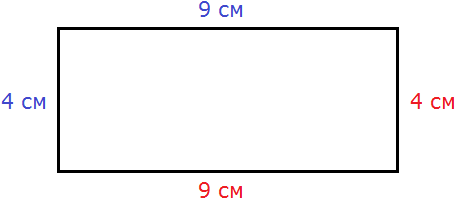
Найдём периметр. Для этого сложим все стороны. Складывать их можно в любом порядке, поскольку от перестановки мест слагаемых сумма не меняется. Периметр часто обозначается заглавной латинской буквой P (англ. perimeters). Тогда получим:
P = 9 см + 4 см + 9 см + 4 см = 26 см.
Поскольку у прямоугольника противоположные стороны равны, нахождение периметра записывают короче — складывают длину и ширину, и умножают её на 2, что будет означать «повторить длину и ширину два раза»
P = 2 × (9 + 4) = 18 + 8 = 26 см.
Квадрат это тот же прямоугольник, но у которого все стороны равны. Например, найдём периметр квадрата со стороной 5 см. Фразу «со стороной 5 см» нужно понимать как «длина каждой стороны квадрата равна 5 см»
Чтобы вычислить периметр, сложим все стороны:
P = 5 см + 5 см + 5 см + 5 см = 20 см
Но поскольку все стороны равны, вычисление периметра можно записать в виде произведения. Сторона квадрата равна 5 см, и таких сторон 4. Тогда эту сторону, равную 5 см нужно повторить 4 раза
P = 5 см × 4 = 20 см
Свойства прямоугольника:
1. Прямоугольник является параллелограммом – его противоположные стороны попарно параллельны.

Рис. 2. Прямоугольник
AB || CD, BC || AD
2. Противоположные стороны прямоугольника равны.
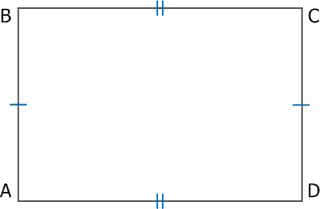
Рис. 3. Прямоугольник
AB = CD, BC = AD
3. Стороны прямоугольника являются его высотами.
4. Прилегающие стороны прямоугольника всегда перпендикулярны.

Рис. 4. Прямоугольник
AB ┴ BC, BC ┴ CD, CD ┴ AD, AD ┴ AB
5. Каждый угол прямоугольника прямой и равен 90 градусам. Сумма всех углов прямоугольника составляет 360 градусов.
Рис. 5. Прямоугольник
∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°,
∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°
6. Диагонали прямоугольника равны.
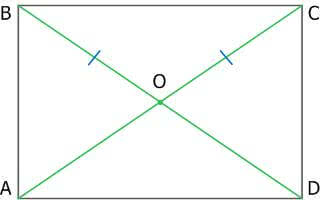
Рис. 6. Прямоугольник
AC = BD
7. Каждая диагональ прямоугольника делит его на два одинаковых прямоугольных треугольника.
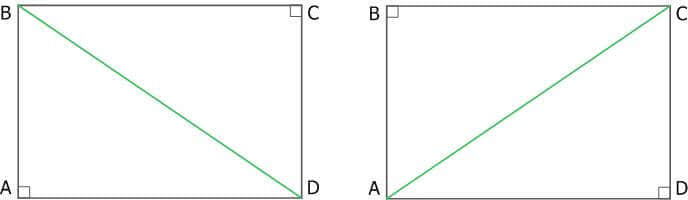
Рис. 7. Прямоугольник
△ABD = △BCD, △ABC = △ACD
8. Квадрат диагонали прямоугольника равен сумме квадратов двух его смежных сторон (что вытекает из теоремы Пифагора).
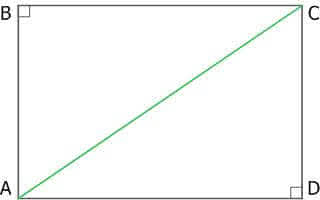
Рис. 8. Прямоугольник
AC2 = AD2+ CD2
9. Диагонали прямоугольника делятся точкой пересечения пополам.
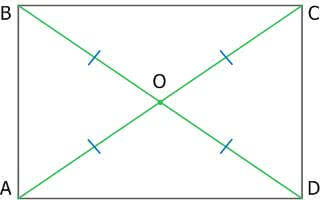
Рис. 9. Прямоугольник
AO = BO = CO = DO = АС2 = BD / 2
10. Около любого прямоугольника можно описать окружность. Диагональ прямоугольника является диаметром описанной окружности.
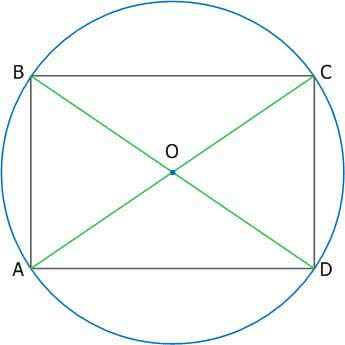
Рис. 10. Прямоугольник
АС и BD – диаметр описанной окружности и диагональ прямоугольника
11. Точка пересечения диагоналей называется центром прямоугольника и является центром описанной окружности.
12. Прямоугольник может содержать вписанную окружность и только одну, если все его стороны равны, т.е. он является квадратом.
Рис. 11. Квадрат
AВ = ВC = AD = CD
Формулы прямоугольника:
Пусть a – длина прямоугольника, b – ширина прямоугольника, d – диагональ и диаметр описанной окружности прямоугольника, R – радиус описанной окружности прямоугольника, P – периметр прямоугольника, S – площадь прямоугольника.
Формула стороны прямоугольника (длины и ширины прямоугольника):
,
,
,
.
Формула диагонали прямоугольника:
,
d = 2R.
Формулы периметра прямоугольника:
P = 2a + 2b,
P = 2(a + b).
Формулы площади прямоугольника:
S = a · b.
Формула радиуса окружности, описанной вокруг прямоугольника:
.
Примечание: Фото https://www.pexels.com, https://pixabay.com
Видео https://www.youtube.com/watch?v=_EVDcbOydAI
Найти что-нибудь еще?
карта сайта
Коэффициент востребованности
2 688
Скрещенные прямоугольники
Пересек четырехугольник (самопересекающийся) состоит из двух противоположных сторон , не являющихся самопересекающегося четырехугольник вместе с двумя диагоналями. Точно так же скрещенный прямоугольник — это скрещенный четырехугольник, который состоит из двух противоположных сторон прямоугольника вместе с двумя диагоналями. У него такое же расположение вершин, как и у прямоугольника. Он выглядит как два идентичных треугольника с общей вершиной, но геометрическое пересечение не считается вершиной.
Пересек четырехугольник иногда сравнивают с галстуком или бабочкой , которую иногда называют «угловые восемь». Трехмерная прямоугольная проволока рама , которая скручивается может принимать форму галстука — бабочки.
Внутренняя часть скрещенного прямоугольника может иметь плотность многоугольников ± 1 в каждом треугольнике, в зависимости от ориентации намотки по часовой стрелке или против часовой стрелки.
Пересек прямоугольник можно считать равноугольным , если правые и левые повороты разрешены. Как и у любого скрещенного четырехугольника , сумма его внутренних углов составляет 720 °, что позволяет внутренним углам выступать снаружи и превышать 180 °.
Прямоугольник и скрещенный прямоугольник — это четырехугольники со следующими общими свойствами:
- Противоположные стороны равны по длине.
- Две диагонали равны по длине.
- Он имеет две линии отражательной симметрии и вращательной симметрии 2-го порядка (до 180 °).
Вычисление диагонали квадрата по известной стороне
Самым простым способом является вычисление диагонали
, если известна сторона квадрата. Здесь действует широко известная теорема Пифагора для прямоугольных треугольников. Запишем эту формулу: c^2 = a^2+b^2.
Отметим, что в нашем случае диагональ квадрата есть гипотенуза треугольника с равными катетами. Перепишем формулу исходя из наших условий: d^2 = a^2+a^2. Преобразуем, получим: d^2 = 2*a^2. Следующим шагом извлечём квадратный корень, получится: d = rad2*a
. Это и есть наша конечная формула.
Рассмотрим вычисление на примере. Пусть a = 64. Подставим наше значение в формулу. Получим d = 64*rad2. Это и есть ответ.